خوارزمية QuickHull

سنتحدث اليوم عن مشكلة معروفة في مجال ال Computational Geometry وهي تحديد أصغر مضلع يحوي مجموعة من النقاط!
وقبل أن ندخل في حل المشكلة ، دعونا نتعرف على بعض المصطلحات .

Points وهي نقاط في المستوى Plane ، مثلا النقاط p(2,2) ,q(3,2),...etc في المستوى R x R ويمكن أن تكون في المستوى الثالث .

Polygon مضلع ، وقد يكون مثلث،مربع،دائرة،....الخ.

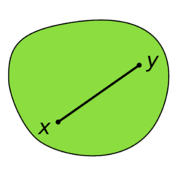
Convex وهو مضلع يحقق الخاصية التالية :

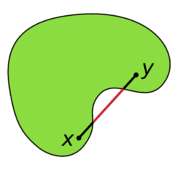
لكل نقطتين فيه p,q فان الخط الواصل بينها يقع داخل هذا الشكل .

Concave هو المضلع الذي لا يحقق الخاصية أعلاه.

Convex Hull هو أصغر مضلع Convex Polygon يحوي مجموعة من النقاط ، وهذا هو ما نريد ان نقوم بانشائه .

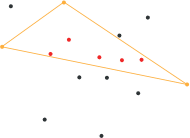
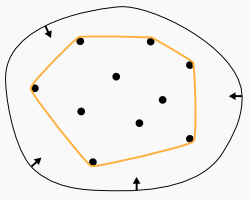
المضلع -باللون البرتقالي- هو ال convex hull .

خوارزمية QuickHull لايجاد الى convex-Hull:

يوجد العديد من الخوارزميات لايجاد هذا المضلع ، وسنذكر هنا خوارزمية QuickHull وهي خوارزمية تعمل بمبدأ Divide and Conquer حيث يتم تقسيم المشكلة الى اجزاء صغيرة -وهكذا يتم التقسيم الى ان نصل الى أصغر جزء ممكن- ثم تحل المشكلة وتجمع الحلول مع بعضها .

وتطبيقها سيكون بالاستدعاء الذاتي ، وهو يعطي كود جميل ومقروء،  لذلك يفضل الكثير هذه الخوارزمية على الرغم من انه توجد بعض الخورازميات الاخرى ذات أداء أفضل لكن بكود أكثر تعقيدا !

وسأشرح الخوارزمية مع مثال نظري لكي تتضح أكثر.

نفرض ان لدينا مجموعة نقاط على المستوى :

الخطوة الاولى : ايجاد أصغر نقطة وأكبر نقطة على المحور الافقي - محور X

ومن ثم نوصل هاتين النقطتين معا .

هاتين النقطتين ستكون داخل المضلع النهائي Proved

هذا الخط سيقسم النقاط الى مجموعتين - فوق الخط وتحت الخط - لكن رياضيا نقول - يسار الخط ويمين الخط-

ونقول أن النقطة p تقع يسار الخط الواصل بين النقطتين u,v اذا كان حاصل الضرب الاتجاهي Cross Product للخط (المتجه) up و uv أكبر من الصفر ، اما اذا كان أقل من الصفر فهذا يعني أن النقطة p تقع يمين الخط (المتجه) uv.

ملاحظة : هناك عدة طرق اخرى لمعرفة مكان النقطة ، وسأستخدم هنا قانون الضرب الاتجاهي.

وكما هو معروف أن حاصل الضرب الاتجاهي لمتجهين هو متجه اخر عمودي على المتجهين ، هذا المتجه وليكن uw لديه اتجاه معين (موجب او سالب) ، ويحدد اتجاه هذا المتجه بناءا على موضع النقطة المراد معرفة مكانها ، فاذا كان المتجه up (الذي طرفه الاخير النقطة p ) يصنع زاوية بعكس عقارب الساعة مع المتجه uv فان حاصل الضرب الاتجاهي سيكون موجب ، اما اذا كان المتجه up يصنع زاوية في اتجاه عقارب الساعة clockwise فان حاص الضرب الاتجاهي مع uv سيكون سالب .

- سأحدث هذه الفقرة لاحقا لكي اضيف بعض الصور التوضيحية وكذلك رموز LaTeX للمعادلات -.

انظر في هذا ال Applet للمزيد :
http://physics.syr.edu/courses/java-suite/crosspro.html

نعود الان الى بقية خطوات الخوارزمية ، وقد وصلنا الى أن هناك مجموعتين من النقاط ، وسنشرح على المجموعة الاولى ، والثانية ستكون بنفس الفكرة.

الخطوة الثانية : ايجاد أبعد نقطة من الخط uv .
حيث أن أبعد نقطة من الخط ستكون داخل المضلع النهائي.

ولايجاد أبعد نقطة من خط ، توجد العديد من الطرق الرياضية ، ساستخدم المعادلة التالية :

- سأحدث هذه الفقرة لاحقا لكي أضيف رموز LaTeX للمعادلات -.

وكما تلاحظ من الشكل السابق ، أبعد نقطة قد شكلت لنا مثلث.

الخطوة الثالثة : استبعاد النقاط الموجودة داخل المثلث .
لانها بالطبع ليست نقاط عظمى Extreme Points

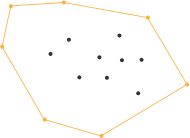
الخطوة الرابعة : كرر الخطوات 2 و 3 !

لان الخوارزمية تعمل بالطريقة التكرارية recursively فكل المطلوب الان هو أن نمسك الضلع (اليمين واليسار) في المثلث كل على حدة ، ثم نقوم بايجاد ابعد نقطة عن الخط وبعدها سيظهر لنا مثلث ، وسنتجاهل النقاط بداخله ، .... وهكذا .

متى سنتوقف ؟

بالتأكيد عندما لا نجد أي نقطة فوق الخط uv مثلا.

الخطوة الخامسة : كرر الخطوات على الجزء الاخر (الذي يقع يمين الخط) ، وهكذا تكون قد انتهت الخوارزمية

تنفيذ الخوارزمية
Implementation of QuickHull in C++/Qt

#ifndef QUICKHULL_H
#define QUICKHULL_H

#include

class QLine;

class QuickHull
{
public:
    QuickHull(const QPolygon &polygon);

    static QPoint minPoint(const QPolygon &polygon);
    static QPoint maxPoint(const QPolygon &polygon);

    const QPolygon &convexHull();

private:
    void findHull(QPoint p1, QPoint p2, QPolygon set);

    static bool isLeft(const QLine &segment, const QPoint &point);
    static int distance(const QPoint &p1, const QPoint &p2, const QPoint &p3);
    static QPoint maxPointDistance(const QPoint &A, const QPoint &B, const QPolygon &set);

    QPolygon m_points;
    QPolygon m_convexhull;
};

#endif // QUICKHULL_H

الفئة QPolygon هي عبارة عن مصفوفة من النقاط .

دالة ايجاد أصغر نقطة :

/* Find the minimum point in the horizontal axis */
QPoint QuickHull::minPoint(const QPolygon &polygon)
{
    QPoint min = polygon.at(0);

    foreach (QPoint p, polygon)
    {
        if (min.x() < p.x())
            min = p;
    }

    return min;
}

ايجاد أكبر نقطة :

/* Find the maximum point in the horizontal axis */
QPoint QuickHull::maxPoint(const QPolygon &polygon)
{
    QPoint max = polygon.at(0);

    foreach (QPoint p, polygon)
    {
        if (max.x() > p.x())
            max = p;
    }

    return max;
}

معرفة مكان النقطة بالنسبة لخط ما ، يمين الخط ام يساره؟

/* Check if point P is left to the line segment AB or not.
** This is done by take the Cross product AB x AP.
** if the result is positive (angle are counter-clockwise) it return true, else return false. */
bool QuickHull::isLeft(const QLine &line, const QPoint &p)
{
    int cp = (line.x2() - line.x1()) * (p.y() - line.y1()) -
             (line.y2() - line.y1()) * (p.x() - line.x1());

    return (cp > 0) ? true : false;
}

حساب أبعد نقطة من خط ما ، لاحظ ان القانون ليس دقيقا فهو يتجاهل الكثير من الاشياء التي لن تأثر على المسافة

/* Compute the (Pseudo)distance between the line segment (p1,p2) and the point p3. */
int QuickHull::distance(const QPoint &p1, const QPoint &p2, const QPoint &p3)
{
    int ux = p2.x() - p1.x();
    int uy = p2.y() - p1.y();

    int s = ux * (p1.y() - p3.y()) - uy * (p1.x() - p3.x());

    if (s < 0)
        s = -s;

    return s;
}

بداية الخوارزمية

/* Start of QuickHull Algorithm */
const QPolygon &QuickHull::convexHull()
{
    if (m_points.size() < 3)
        return m_points;

    // Find the min/max point in the convex polygon
    QPoint A = minPoint(m_points);
    QPoint B = maxPoint(m_points);

    QLine segment(A, B);

    // Add min/max point to the m_convexhull
    m_convexhull << A << B;

    // Remove min/max from the set of all points m_points
    m_points.remove(m_points.indexOf(A));
    m_points.remove(m_points.indexOf(B));

    // Find the left and right points lies with the line segment (A,B).
    // This line divide the hull into upper and lower hull.
    QPolygon upperHull;
    QPolygon lowerHull;

    foreach (QPoint p, m_points)
    {
        if (isLeft(segment, p))
            upperHull << p;
        else
            lowerHull << p;
    }

    findHull(A, B, upperHull);
    findHull(B, A, lowerHull);

    return m_convexhull;
}

الدالة التكرارية - تقسيم المشكلة وجمع الحلول هنا-

void QuickHull::findHull(QPoint A, QPoint B, QPolygon set)
{
    // Place to put the new extreme point
    int index = m_convexhull.indexOf(B);

    if (set.size() == 0)
        return;

    if (set.size() == 1)
    {
        QPoint p = set.at(0);
        set.remove(set.indexOf(p));
        m_convexhull.insert(index, p);
        return;
    }

    // Find point that maximize the area of the triangle.
    QPoint C = maxPointDistance(A, B, set);

    // Add this point to the convex hull(proved)
    set.remove(set.indexOf(C));
    m_convexhull.insert(index, C);

    // Add points left of AC to leftAC set and add points left of CB to leftCB
    // This will automatically discard all points inside this triangle ACB.

    QPolygon leftAC;
    QPolygon leftCB;

    foreach (QPoint q, set)
    {
        if (isLeft(QLine(A, C), q))
            leftAC << q;
    }

    foreach (QPoint r, set)
    {
        if (isLeft(QLine(C, B), r))
            leftCB << r;
    }

    findHull(A, C, leftAC);
    findHull(C, B, leftCB);
}

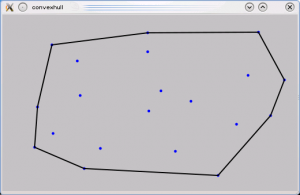
وفي الملف المرفق ستجد مثال بسيط Quick & Dirty، وكل ما عليك ان تحدد مجموعة من النقاط ثم تضغط على زر start وسيتم تحديد ال convex hull.

تطبيقات على الخوارزمية :
Computer Visualization, Ray Tracing, Video Games, Replacement of Bounding Boxes
Path Finding - Embedded AI of Mars mission Rovers
Geographical Information Systems (GIS) - Computing Accessibility Maps
Visual Pattern Matching - Detecting Car License Plates
Verification Methods - Bounding of Number Decision Diagrams
Geometry - Diameter Computation

http://www.tcs.fudan.edu.cn/rudolf/Courses/Algorithms/Alg_ss_07w/Webprojects/Chen_hull/applications.htm

روابط :
http://en.wikipedia.org/wiki/Convex_hull
http://westhoffswelt.de/blog/0040_quickhull_introduction_and_php_implementation.html
http://www.cse.yorku.ca/~aaw/Hang/quick_hull/Algorithm.html
http://www.ahristov.com/tutorial/geometry-games/convex-hull.html

مرفق:
convexhull.tar