السلام عليكم و رحمة الله و بركاته
في هذه المقالة, سأضع بين أيديكم شرحا لخوارزمية Diffie-Hellman و كلي أمل بأن يستفيد الجميع.
قمتُ بإدخال بعض الروابط المهمة في بعض الكلمات للذين يريدون الاستزادة, الكتابة المُظللة, ذات اللون الأزرق تدل على وجود رابط, مثل هذه الكتابة انفورماتيك.
فهرس المقالة :
- مُقدمة
- ما هو التشفير ؟
- التشفير في العصر القديم
- التشفير الحديث
- نظرة تحليلية على الخوارزمية
- فكرة الخوارزمية
- البروتوكول
- مثال تطبيقي
- التعقيد الزمني
- الخاتمة
- المراجع
1. مُقدمة
- 1.1 ما هو التشفير ؟
- 1.2 التشفير في العصر القديم
- 1.3 التشفير الحديث
1.1 – ما هو التشفير ؟
هو عملية يتم فيها إخفاء المعلومات عن طريق مفتاح سري وخوارزمية, حيث يمكن للشخص الذي يعرف المفتاح و خوارزمية التشفير, فك الشفرة ( أي استعادة المعلومات الأصلية), يمكن أيضاً أن يقوم شخص آخر لا يعرف المفتاح و لا الخوارزمية بفك الشفرة !! و تُسمى العملية هنا “عملية غير مخولة”.
في عام 1900 قبل الميلاد لم تكن هناك سوى مصطلحات هيروغليفية, استخدم الإنسان التشفير منذ حوالي ألفي عام قبل الميلاد لحماية رسائله السرية, وبلغ هذا الاستخدام ذروته في فترات الحروب, خوفا من وقوع الرسائل الحساسة في أيدي الأعداء, فالحروب دائما كانت الملهم الأكبر لظهور خوارزميات التشفير.(1)
1.2 – التشفير في العصر القديم
يُعد علم التشفير من أقدم العلوم الموجودة في يومنا هذا حيث تمتد أصوله إلى زمن الفراعنة و القياصرة أيضا, فقد كان الفراعنة أول من قام بعملية التشفير للتراسل بين قطاعات الجيش, دون أن ننسى أن أفضل طريقة استُخدمت في القدم هي طريقة يوليوس قيصر (Julius Caesar) وهو أحد قياصرة الروم, كما استخدم الصينيون القدامى طُرقا عديدة في علم التشفير والتعمية لنقل الرسائل السرية أثناء الحروب, فقد كانوا يستخدمون التشفير من أجل إخفاء الشكل الحقيقي للرسائل حتى لو سقطت في يد العدو فإنه يصعب عليه فهمها.
كما يُعتبر علماء المسلمين و العرب أول من اكتشف طرق استخراج المعمَّى(2), من أشهرهم العلامة يعقوب بن إسحاق الكندي و ابن وَحشِيَّة النبطي الذي كشف اللثام عن رموز الهيروغليفية قبل أن يكتشفها العالم الفرنسي Jean-François Champollion بعشرة قرون !! (3), و كذلك اشتهر ابن دريهم الذي كان لا يشق له غبار في فك التشفير فكانت تُعطى له الرسالة معماة فما إن يراها حتى يحولها في الحين إلى العربية ويقرئها .. وله قصيدة طويلة يشرح فيها مختلف الطرق في تعمية النصوص وكان يحسن قراءة الهيرغليفية.(4)
يعتبر البعض أن طريقة الألغاز كانت من أوائل الطرق الـُمستخدمة قديما في التشفير, فكانوا يأخذون جملة, مثل (ادفع لي أجرا ) ويدخلون كل حرف في بداية كلمة جديدة فتصبح (إذا دخل فاروق عليه لباس يبدو أكثر جمالا راتبه أكثر) وللحصول على الجملة المطلوبة نأخذ الحروف التي تبدأ بها كلمات الجملة الجديدة فنحصل على (ادفع لي أجرا).
لكن هذه الطريقة صعبة جداً خاصة إذا كانت حجم المعلومات المـُراد إرسالها كبيراً حيث تكمن صعوبتها في إيجاد جمل تحمل المعلومات المطلوبة ولها مدلول واضح لا يثير الشك، لذا فإن هذا النوع نادراً ما يُستخدم في الوقت الحالي.
1.3 – التشفير الحديث
في العصر الحديث, تُعد آلة Enigma التي استخدمها الجيش الألماني في الحرب العالمية الثانية, أبرز مثال على استخدام التعمية لتحقيق تفوق على العدو في مجال الاتصالات، وكانت الأبحاث التي جرت بشكل منفصل في كل من المؤسستين العسكريتين الأمريكية والبريطانية في سبعينيات القرن العشرين فتحا جديدا فيما صار يعرف الآن بتقنيات التعمية القوية المعتمدة على الحوسبة، وارتبطت التعمية بعلوم الجبر ونظرية الأعداد ونظرية التعقيد ونظرية المعلوماتية.
في نهاية السبعينات من القرن المنصرم, و مع الاستخدام المـُكثف لأجهزة الكمبيوتر, دخل علم التشفير مرحلة جديدة حيث أصبح البعض يُسميه “التشفير الحديث” (Modern cryptography) و مع التطور السريع الذي يشهده مجال الحماية و الأمن, أصبحت الحاجة ملحة لطرق تشفير قوية, لأن زيادة سرعة الكمبيوتر تعني قصر الوقت الذي يحتاجه الأخير لكسر أو كشف مفتاح تشفير معين.
يرجع الفضل في إظهار مفهوم التشفير الغير متناظر إلى الرائدين Whitfield Diffie و Martin Hellman, حيث قدَّما هذا المفهوم لأول مرة في المؤتمر الوطني للحاسوب في عام 1976 (5) قبل أن يتم نشره بعد بضعة أشهر (6) في “التوجهات الجديدة في علم التشفير” (New Directions in Cryptography).
يظل المخترع الأب مُختفيا خلف الكواليس – كما يحدث دائما في تاريخ التشفير – إذْ يعتبر البعض (7) أن الباحث الأمريكي Ralph Merkle هو أول من اكتشف فكرة “تشفير المفتاح العام” (Cryptography Asymmetric) بشكل مستقل, رغم أن كتاباته (8) عن الموضوع لم تُنشر إلا مؤخرا.
لم يستطع كل من W. Diffie و M. Hellman تقديم مثال حي على نظام المفتاح العام في البحث الذي قدماه سنة 1976. كان يجب عليهم أن ينتظروا سنة 1978 للحصول على مثال واقعي(9) مُقدم من طرف الثلاثي المميز : Adi Shamir, Ronald Rivest and Leonard Adleman
2. نظرة تحليلية على الخوارزمية
- 2.1 – فكرة الخوارزمية
- 2.2 – البروتوكول
- 2.3 – مثال تطبيقي
- 2.4 – التعقيد الزمني
2.1 – فكرة الخوارزمية
تُعتبر خوارزمية D-H الأول من نوعها في موضوع تبديل المفاتيح, حيث تسمح لشخصين (عادة ما يُطلق عليهما Alice و Bob) بتبادل بيانات حساسة دون أن يفهمها الطرف الثالث (المتصنت) حتى و لو حصل على نسخة منها. تعتمد الخوارزمية في عملها على إنشاء مفتاح سري مشترك يمكن استخدامه فيما بعد لتشفير المحادثات باستخدام خوارزمية تشفير مفتاح متماثل Symmetric-key.
2.2 – البروتوكول
- ليكن n و B العددان الصحيحان اللذان اختارهما كل من Alice و Bob علناً, n و B يجب أن يكونا أوليين فيما بينهما.
- سريا, تختار Alice بدورها عددا صحيحا بشكل عشوائي, نُسميه a, ثم تحسب العدد
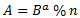
- يقوم Bob بنفس الحركة السابقة: يختار بشكل سري عددا عشوائيا g ثم يحسب
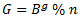
- من الآن فصاعدا, كل طرف يملك نتيجة حساب الآخر, Alice ما عليها سوى حساب
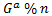
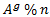
في الحقيقة, فإن العددان السابقان متساويان :
الآن, أصبح Alice و Bob يمتلكان العدد 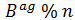
لكن, كيف يمكن هذا ؟؟
لا يُمكن للطرف الثالث (المتصنت) أن يعرف العدد a أو g (هذا العددان ضروريان لإيجاد العدد 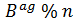
كيف تتأكد Alice من وصول الرسالة إلى Bob و عدم تحريفها ؟
عندما تُرسل Alice رسالة سوف يتم تشفيرها بالمفتاح الخاص بها أو المفتاح العام التابع لــ Bob، بحيث تتحول هذه الرسالة إلى رموز لا يمكن فهمها ويتم إرفاق معها توقيع المـُرسل.
عند إذن يقوم المستقبل بإرسال نسخه من التوقيع الالكتروني إلى الجهة المختصة بإصدار الشهادة، لتتأكد من صحة التوقيع ومن ثم تقوم أجهزة الكمبيوتر التابعة للجهة المختصة بالتحقق من صحة التوقيع وتُعاد النتيجة للمستقبل مرة أخرى، ليتأكد من صحة وسلامة الرسالة، فيقوم المستقبل بقراءة الرسالة وذلك باستخدام مفتاحه الخاص إذا كان التشفير قد تم على أساس رقمه العام أو بواسطة الرقم العام للمرسل إذا تم التشفير بواسطة الرقم الخاص للمرسل، ومن ثم يجيب على المرسل باستخدام نفس الطريقة وهكذا تتكرر العملية، و يُستخدم أيضا مع التوقيع الالكتروني عملية الهاش التي توفر تكلفة أقل من تشفير الرسالة بحيث تقوم بإنشاء قيمة رقمية معينة تكون أصغر من الرسالة بحيث تضمن عدم تغييرها, عندما يستقبل المستخدم الرسالة و الهاش يقوم بعملية الهاش مرة أخرى على هذه الأخيرة ومن ثم يقارن ما بين الهاش الأصلي و الهاش المـُستقبل, إذا كانت القيم متساوية فهذا يدل على سلامة البيانات من التحريف والتزوير وإذا اختلفت القيم دل ذلك على تزوير الرسالة. (10)
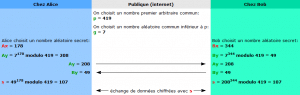
2.3 – مثال تطبيقي
الجزء الأخضر يُمثل البيانات العامة التي يتم تبادلها أمام الجميع بينما يُمثل الجزء الأحمر البيانات الخاصة بكل طرف:
يُمكن لــ Alice و Bob أن يستخدما العدد 107 كمفتاح لتشفير الرسائل المـُتبادلة بينهما (11), عمليا نستخدم أعداد ضخمة جدا و لكن الهدف هنا هو توضيح الفكرة فقط.
2.4 – التعقيد الزمني
عند تطبيق الخوارزمية سيتم حساب أربع exponentiations mod p, باستخدام خوارزمية الأس المعياري السريع فإن وقت التنفيذ يتغير بتغير حجم العدد p الذي عادة ما يكون عددا أوليا ضخما. (12)
إذا أردنا تبادل مفتاح حجمه L سيكون عدد الـ binary operations يساوي 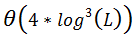
3. الخاتمة
إلى هنا أصل بك أخي القارئ إلى نهاية هذه الجولة السريعة, بالطبع الموضوع شيق و يحتاج إلى الكثير من الشرح, ما زالت هناك العديد من النقاط التي كنت أود التحدث عنها (لكن أخاف أن يزيد الحجم عن حجم المقالة القياسي) مثل كتابة الخوارزمية بلغة الــ Java أو السي++ و إدراج خوارزمية DSS في D-H من أجل إضافة التواقيع الرقمية (Digital signature) إلى البيانات المـُتبادلة و الكثير الكثير من النقاط المهمة التي ربما أكتب عنها لاحقا.
4. المراجع
(1) : ما هو التشفير ؟ – موسوعة الأسئلة والإجابات الحرة
(2) : THE CODEBREAKERS, David Kahn, page 93 ; Kahn on Codes, David Kahn, page 41
(3) : كتاب علم التعمية واستخراج المعمَّى عند العرب
(4) : ابن الدريهم وجهوده في علم التعمية (التشفير), الدكتور محمد حسان الطيان
(5) : W. Diffie and M.E. Hellman, Multiuser cryptographic technics, Proceedings of AFIPS National Computer Conference, 109-112, 1976
(6) : W. Diffie and M.E. Hellman, New directions in cryptography, IEEE transactions on information theory, 22(1976), 644-654
(7) : A.J. Menezes, P.C Van Oorschot, S.A. Vanstone, Handbook of applied cryptography, CRC Press, 1997, p47
(8) : R.C. Merkle, Secure communications over insecure channels, Communications of the ACM, 21(1978),294-299
(9) : Ronald Rivest, Adi Shamir, Leonard Adleman, A Method for Obtaining Digital Signatures and Public-key Cryptosystems, Communications of the ACM, 21(1978), 120-126
(10) : التوقيع الالكتروني .. خطوة إلى الأمام, جريدة الخليج الإماراتية – الملحق الاقتصادي
(11) : Exemple d’algorithme asymétrique : Diffie-Hellman
(12) : La Naissance de la Cryptographie Asymétrique, Guénaël Renault, SALSA – LIP6/UPMC – 14 mars 2012
تحياتي.





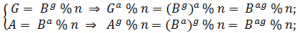


شكرا لك على هذه المقالة الرائعة , موضوع شيق جداا وبه تفاصيل يمكن التعمق والبحث فيها , من النادر ان اجد شرح لمثل هذه الامور بالعربية
شكرا لك اخي العزيز على هذا الموضوع الشيق … جعله الله في ميزان حسناتك..
لدي سؤال وهو ان ال (Diff-Hellman)تستخدم في عملية المصادقة Authentication .هل يوجد خوارزمية اقوى منها في هذا المجال . مع جزيل الشكر والامتنان
شكرا لك اخي العزيز …جعله الله في ميزان حسناتك…لدي سؤال هل ان استخدام خوارزمية Diffie-Hellm تعتبر الافضل بالنسبة ل (Authentication ) او خوارزمية(RSA) افضل منها او يوجد خوارزميات اخرى اكفء من الاثنين…وهل يوجد الكود بلغة (JAVA) او (PHP) لكتابه هذه الخوارزميات…مع جزيل الشكر وبارك الله فيك .