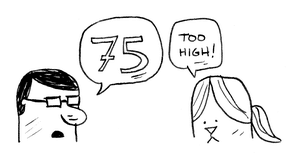افترض انك تبحث عن شخص فى دليل التليفون وكان اسمة يبدأ بحرف الكاف (بالطريقة التقليدية) فأنت تبدأ بفتح الدليل وتبحث من الصفحة الاولى وتقلب الصفحات الى أن تصل للصحفة التى بها حرف الكاف . لكن كان من الافضل ان تبدأ من منتصف الدليل لانك تعلم أن حرف الكاف ليس من الحروف الاولى فى الترتيب الابجدى
افترض انك مسجل فى Facebook عندما تقوم بعمل دخول sign in فأن Facebook يجب ان يتأكد ان اسم المستخدم موجود لدية فى الdatabase اى يبحث عنة ومن الافضل ان يبدأ البحث فى الdatabase من نقطة فى الوسط
هذة التطبيقات وغيرها كثير عبارة عن مشاكل بحثsearch problem تستخدم او تحتاج لاستخدام خوارزمية binary search لحلها.
Binary search هى عبارة عن خوارزمية المدخل لها عبارة عن قائمة بها عناصر مرتبة والمخرج منها عبارة عن موقع العنصر الذى تبحث عنة
مثال:
لكى نفهم كيف تتم العمليات فى binary search المثال عبارة عن لعبة التخمين وفيها اعطيك قائمة مرتبة بها الارقام من 1 الى 100
وانت عليك ان تخمن الرقم الذى اخترتة فى اقل عدد من التخمينات وكل مرة تقوم بتخمين رقم سوف ارشدك بأننى اقول لك الرقم كبير جدا too high او صغير جدا too low او صحيح correct
لنبدأ :
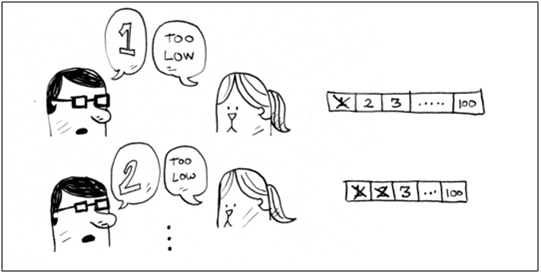
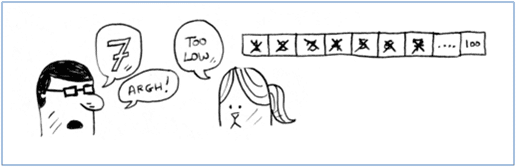
كما بالصورة الرقم الصحيح هو 7 وقام اللاعب بتخمين رقم واحد فكانت الاجابة too low
ثم قام اللاعب بتخمين الرقم 2 وكانت الاجابة too low فقام بالغاؤة الى ان وصل اللاعب للرقم 7 وهو الرقم الصحيح , نلاحظ فى هذة الطريقة انك بدأت من البداية للقائمة بالرقم واحد وعندما كان خطأ خذفتة وقلت الرقم الذى يلية وهكذا الى ان تصل للرقم الصحيح .
ان تبدأ بالرقم فى الوسط middle وليكن 50 فتكون الاجابة too low لذلك انت تقوم بالغاء الارقام من 1 الى 50 دفعة واحدة
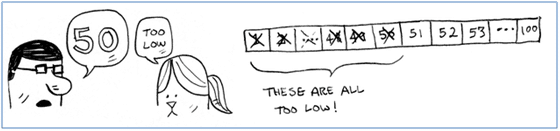
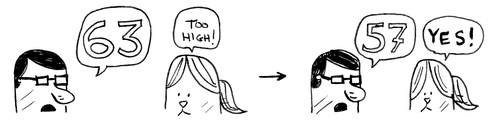
مرة اخرى تقم بالغاء الارقام من 75 الى 100 وتكون الارقام المرجح انها صحيحة بين 51 الى 74 وهكذا الى ان تصل للرقم الصحيح
هذة هى خوارزمية البحث الثنائى لو اردنا حساب كم رقم ممكن ان نحذفة فى كل خطوة iteration
فمهما كان الرقم الذى افكر فية فيمكنك ان تستنتجة فى 7 خطوات iteration فقط لانك فى كل مرة تخمن فيها رقم سوف تقوم بالغاء نصف الارقام .

فى الخوارزمية العادية فى اسوء الحالات لو كانت الكلمة اخر كلمة فى القاموس فسوف تأخذ 240,000 خطوة لايجاد الكلمة اما خوارزمية البحث الثنائى ففى كل خطوة سوف تقوم بتقسيم الكلمات الى نصفين وتلغى احدهما الى ان تصل الى كلمة واحدة فقط

بصورة عامة فأن خوارزمية البحث الثنائى اذا كان لدى قائمة مكونة من n عنصر فهى تأخذ عدد من الخطوات بمقدار log2 n لايجاد اى عنصر فى قائمة
ملحوظة :
عند استخدام خوارزمية البحث الثنائى يجب ان تكون العناصر فى القائمة مرتبة sorted list
Running time
عند التحدث عن اى خوارزمية يجب ان نتحدث عن كفائتها من حيث إما :
- الوقت running time
- أو المساحة فى الذاكرة space
بالنسبة لخوارزمية البحث الثنائى كم هو الوقت الذى نحفظة عند استخدامها ؟
لو نظرنا الى الخوارزمية العادية نجد اننا نختبر كل عنصرمرة تلو الاخرى اى اذا لدينا قائمة بها 100 عنصر فسوف نخمن 100 مرة واذا لدينا قائمة بها 4 بليون عنصر سوف نخمن 4 بليون مرة اى عدد التخمينات يكون مساوى لحجم القائمة ونطلق على ذلك ان الخوارزمية تعمل فى linear time او O(n)
فى خوارزمية البحث الثنائى الامر مختلف اذا لدينا قائمة بها 100 عنصر سوف يكون عدد التخمينات 7 مرات واذا لدينا قائمة بها 4 بليون عنصر سوف يكون عدد التخمينات 32 مرة اى ان الخوارزمية تعمل فى log time اى O(log(n)) كما موضح بالشكل
الكود بالبايثون:
اذا اردنا كتابة الكود للبحث عن رقم ما بالقائمة -فهذا الكود يبحث عن رقم 3 بالقائمة
[1, 3, 5, 7, 9]
def binary_search(list, item): low = 0 high = len(list)—1 while low <= high: mid = (low + high)//2 guess = list[mid] if guess == item: return mid if guess > item: high = mid - 1 else: low = mid + 1 return None my_list = [1, 3, 5, 7, 9] print binary_search(my_list, 3) # => 1 print binary_search(my_list, -1) # => None
الكود بالجافا
public static int binarySearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
int midVal = a[mid];
if (midVal < key)
low = mid + 1
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
رجاء:لا تنسونى من الدعاء عن ظهر غيب
رَبِّ إِنِّي لِمَا أَنزَلْتَ إِلَيَّ مِنْ خَيْرٍ فَقِيرٌ
الحمد الله رب العالمين والصلاة والسلام على أشرف المرسلين سيدنا محمد صلى الله علية وسلم وعلى اله وصحبة وسلم -اللهم دومها نعمة وأحفظها من الزوال -أمين