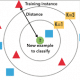
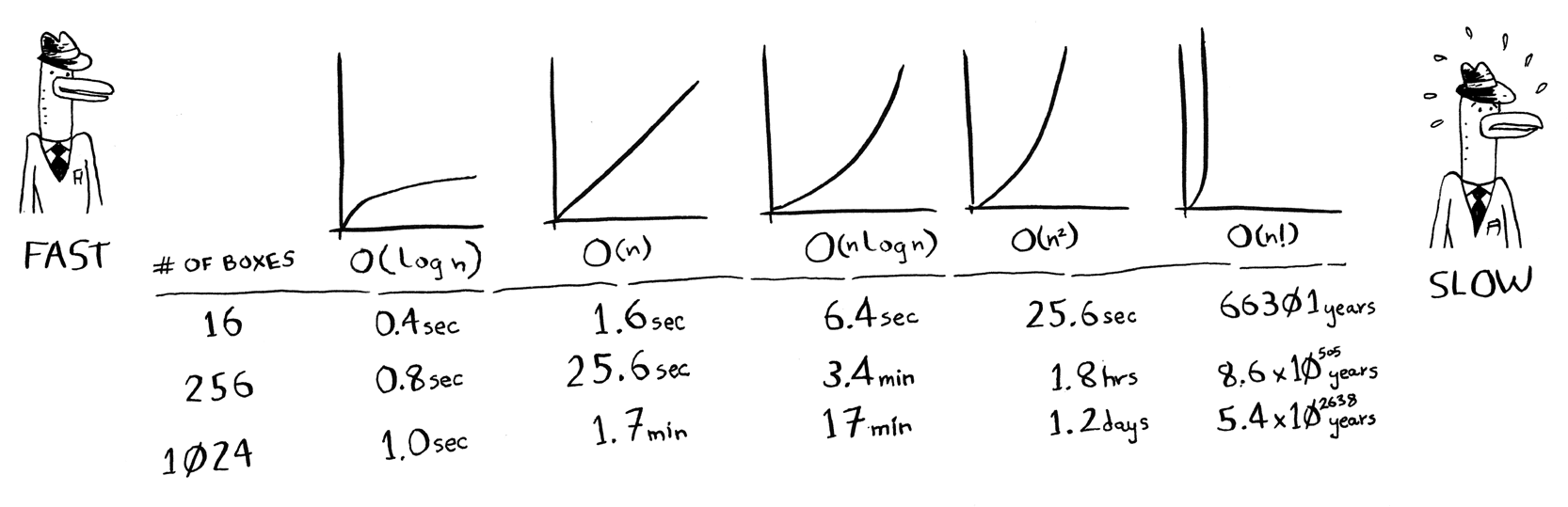قياس كفاءة أى خوارزمية أو ادائها يعتمد على عدة عوامل:
1-الوقت CPU (time)
2-الذاكرة memory usage
3- المساحة فى الهارد disk usage
4- الشبكة network usage
كل هذة العوامل مهمة وسوف نتحدث فى هذة المقالة عن الوقت CPU (time)
بداية لنكن حذرين فهناك فرق كبير بين:
1-الاداء Performance :وهى تعرفك كم هو الوقت اللازم time /الذاكرة memory /المساحة فى الهارد disk /.. المستخدمين فعليا عند تشغيل البرنامج لحل مشكلة ما وهذة الاشياء تعتمد على الجهاز والمعالج compiler,وأيضا الكود.
2-التعقيد للخوارزمية Complexity:سوف تخبرك ماذا يحدث وما هو الوقت اللازم والresources اللازمة لعمل الخوارزمية او البرنامج اذا زاد حجم المشكلة size of problem
Big O هى طريقة تخبرك مدى تعقيد الخوارزمية complexity of an algorithm
وعندما نتحدث عن complexity of an algorithm فنحن لا نهتم بالوقت اللازم للخوارزمية ولا عدد الخطوات فقط بل نهتم بالعلاقة بين عدد الخطوات اللازمة للخوارزمية number of operations or steps نسبة الى حجم المشكلة problem sizeاو حجم المدخلات
لكن من يهتم ؟
حسنا فى الغالب أنت سوف تستعمل خوارزميات لاشخاص أخرين ولكن حتى فى هذة الحالة من الجيد ان تعرف مدى complexity لتلك الخوارزميات لتختار ايهم افضل لحل مشكلتك
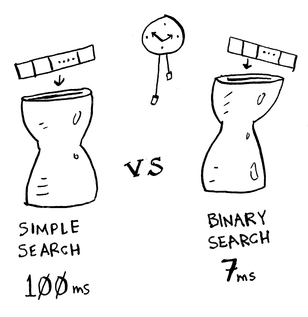
لنفترض ان dr savealife يعمل لدى شركة ناسا NASA واراد ان يكتب خوارزمية للبحث عن المكان الذى سوف يهبط فية الصاروخ على سطح القمر .مع العلم أن شركة ناسا طلبت ان تكون الخوازمية التى سوف يستخدمها يجب ان تكون صحيحة وتعمل بشكل جيد وفى نفس الوقت سريعة تعطية النتائج فى مدة لا تزيد عن الـ 7 ثوانى
dr savealife الان يقارن هل يستخدم خوارزمية البحث العادى ام البحث الثنائى ؟ وقال اذا استخدمت البحث الثنائى سوف يجد مكان هبوط الصاروخ بسرعة وفى وقت قصير لكن الكود ممكن يكون بة اخطاء فلا يمكن تحديد المكان بشكل صحيح اما خوارزمية البحث العادى فكتابة الكود سوف تكون اسهل وليس بة اخطاء ولكن الوقت سوف يكون كبير هو قرر ان يختبر الخوارزميتين اولا على قائمة بها 100 عنصر ليرى الوقت الذى سوف تستغرقة كل خوارزمية
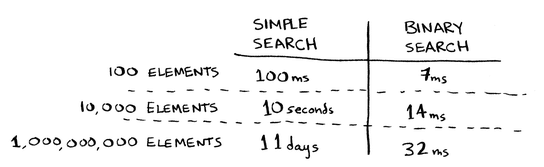
لو افترضنا ان الزمن اللازم لاختبار كل عنصر فى القائمة هو واحد ملى ثانية millisecond فخوارزمية البحث العادى سوف تأخذ 100 ملى ثانية millisecond إما خوارزمية البحث الثنائى سوف تأخذ 7 ملى ثانية لان log2 100 مساوى 7
dr savealife قرر أن يستخدم الخوارزمية العادية لانها سهلة فى كتابة الكود ايضا هى تحقق الشرط لشركة ناسا ان تعمل الخوارزمية فى مدة لا تتعدى 7 ثوانى-طبعا هو قام بخطأ كبير لانة لم يضع فى الحسبان ماذا اذا كبر space للبحث ما هى نتيجة اختيارة للتوضيح :
ماذا اذا كانت القائمة بها عناصر اكثر بدل من 100 عنصر لنجعلها 1 بليون عنصر سوف نجد ان الخوارزمية العادية سوف تأخذ 1 بليون ms اى 11 يوم إما خوازمية البحث الثنائى سوف تأخذ 32 ms وفى هذة الحالة الفرق كبير بين الخوارزميتين
اى معنى ذلك انة كلما زادت العناصر او زاد مجال البحث كلما كانت خوارزمية البحث الثنائى افضل واسرع ولذا كان علينا ليس معرفة ما هى سرعة الخوارزمية فقط بل ما مدى كفاءة الخوارزمية عند زيادة مجال البحث من هنا جاءت طريقة الـbig O
Big O طريقة تخبرك ما هو مدى سرعة برنامجك او خوارزميتك نسبة الى عدد الخطوات فية iteration عندما يزيد حجم المشكلة. فمثلا فى الخوارزمية العادية لاختبار كل عنصر بقائمة تحتوى على عدد n عنصر سوف يكون لديك n خطوة اى O(n) ما هو الوقت اللازم بالثوانى Big O لا تحسب الوقت بالثوانى بل بالخطوات فمقارنة البرامج الان سوف تكون على اساس كم خطوة iteration سوف يأخذ برنامجك لايجاد النتيجة .
مثال اخر خوارزمية البحث الثنائى تحتاج الى log n خطوة لكى تختبر قائمة بها n عنصر لذا نقول ان big O لها هى O(log n) اى ان الخوارزمية تأخذ log n خطوة
كيف تعمل الـbig O :
لتصور كيف تعمل الbig O سوف نختبرها على اكثر من خوارزمية ونرى كيفية حسابها بمثال عملى بسيط يحتاج فقط ورقة صغيرة وقلم لنبدأ: لو قلت لك ارسم 16χ16 مربع هل تستطيع؟
انك سوف ترسم مربع مربع كما بالشكل التالى
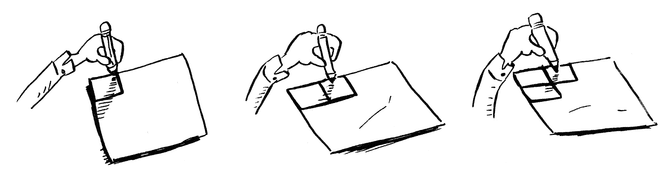
الخوارزمية الثانية :
انك تقوم بعمل ثنى fold للورقة كما بالشكل فى المرة الاولى تجد انك حصلت على مربعين من خطوة واحدة ثم بتكرار عملية الثنى
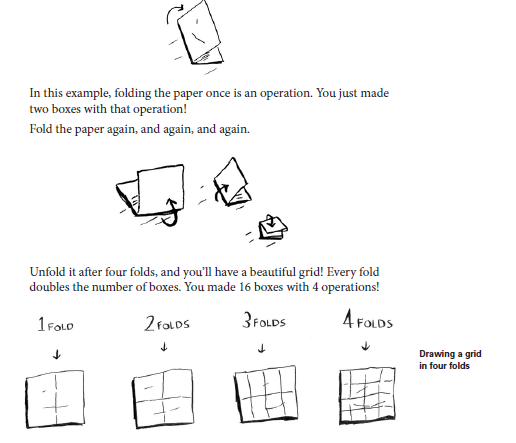
كيف نحسب نسبة التعقيد للخوارزمية how to determine the complexities
كثير من يسأل كيف احسب big O لاى خوارزمية الان سوف نكون مثل الجراحين جزء جزء لنتعلم ولنأخذها على حالات :
1-الحالة الاولى: اذا لدى تتابع من الجمل Sequence of statements
statement 1; statement 2; ... statement k;
فلو كل statement اخذت وقت معين فسيكون الوقت الكامل عبارة عن مجموعهم
total time = time(statement 1) + time(statement 2) + … + time(statement k)
ولوكانت العملية بسيطة مثل(جمع -ضرب -قسمة ..) فأن الخوارزمية تكون O(1) اى a constant-time algorithm
2-الحالة الثانية :اذا كان هناك جمل شرطية IF
if (cond) then block 1 (sequence of statements) else block 2 (sequence of statements) end if;
فى هذة الحالة سوف نحسب حسب الblock الذى سوف يقوم بعمليات اكثر لانها اللحالة الاسوء اى سوف نأخذ max(time(block 1), time(block 2))
3-الحالة الثالثة: لو هناك تكرار Loops
for I in 1 .. N loop sequence of statements end loop;
فى هذة الحالة الloop سوف تكون N مرة لذا ايضا مجموعة statements سوف تتكرر N مرة
لو اعتبرنا ان كل statement تنفذ O(1) فيكون قيمة التعقيد الكلى N * O(1) اى مساوية O(N)
4-الحالة الرابعة: التكرار المتداخل Nested loops
for I in 1 .. N loop for J in 1 .. M loop sequence of statements end loop; end loop;
فى هذة الحالة الloop الخارجية outer loop سوف يتم تنفيذها N مرة وفى كل مرة تنفذ الloop الداخلية inner loop عدد M مرة فبذلك يكون التعقيد O(N * M).
5-الحالة الخامسة:المناداة على ميثود Statements with function/ procedure calls
for J in 1 .. N loop g(J); end loop;
فى هذة الحالة لدى outer loop سوف تتنفذ N مرة وفى كل مرة تنادى على ميثود function لا تنزعج كل ما عليك معرفة التعقيد للfunction فاذا كان مثلا N فسيكون التعقيد الكلى O(N2)
بعض Big O run times الشائعة:
1-O(1): وتعرف بأنها ثابتة a constant-time algorithm
2-O(log n): وتعرف ايضا بأسم log time ومن امثلتها خوارزمية البحث الثنائى
3-O(n): وتعرف ايضا بأسم linear time ومن امثلتها البحث البسيط او العادى
4-O(n * log n): وهى تعتبر سريعة نسبيا ومن امثلتها خوارزميات الترتيب السريعة مثل quick sort
5-O(n2): وهى بطيئة ومن امثلتها خوارزميات الترتيب البطيئة مثل selection sort
6-O(n!): وهى تعتبر بطيئة جدا ومن امثلتها traveling salesperson
مراجع:
http://web.mit.edu/16.070/www/lecture/big_o.pdf
رجاء:لا تنسونى من الدعاء عن ظهر غيب
رَبِّ إِنِّي لِمَا أَنزَلْتَ إِلَيَّ مِنْ خَيْرٍ فَقِيرٌ
الحمد الله رب العالمين والصلاة والسلام على أشرف المرسلين سيدنا محمد صلى الله علية وسلم وعلى اله وصحبة وسلم -اللهم دومها نعمة وأحفظها من الزوال -أمين