خوارزمية K-Nearest Neighbor

تخيل أنك تحاول أن تتنبأ من هو الرئيس الذى سوف أنتخبة فى الانتخابات القادمة . أذا أنت لا تعرف أى شىء عنى سوى أين أسكن فمن الأمور المرجح أن تفعلها أنك سوف تنظر إلى جيرانى وتعرف من سينتخبوا؟

هذا هو أساس خوارزمية K-Nearest Neighbour algorithm

Nearest Neighbors هى أحد خوارزميات التنبؤ Predictive Model وهى لاتحتاج الى تعلم معادلات رياضية معقدة بل تحتاج فقط إلى توفر شيئن فى البيانات DataSet:

طريقة لحساب المسافة distance بين البيانات
تحقيق افتراضية أن البيانات القريبة من بعضها تكون متشابهة والبعيدة عن بعضها تكون غير متشابهة؟

معظم التقنيات التى تستخدم فى خوارزميات التنبؤ Predictive Model تنظر الى مجموعة البيانات ككل من أجل معرفة أنماط البيانات لكن Nearest neighborsمن ناحية أخرى تهمل الكثير من المعلومات حيث ان فيها يتم التنبؤ لكل نقطة جديدة(مثال جديد new instance) اعتمادا فقط على عدد النقاط القريبة منها.

الخوارزمية خطوة بخطوة:

1-نحدد قيمة المتغير k الذى يعبر عن عدد المجاورين

2-نحسب قيمة المسافة بين المثال الجديد والامثلة التى فى dataset

3-نرتب الامثلة لنحصل على المجاورين أعتمادا على أقل مسافة تم حسابها فى الخطوة السابقة ونأخذ منهم عدد k مجاور

4-نحدد الكلاس للمجاورين

5-الكلاس الاكثر اغلبية للمجاورين هو الكلاس المتوقع لهذا المثال

اى الخوارزمية بأختصار “Tell me who your neighbors are, and I’ll tell you who you are”

مثال بسيط لتوضيح طريقة عمل الخوارزمية:

نفترض ان لدينا مصنع يقوم بصنع الاقلام وقمنا بعمل إستطلاع عن جودتهم من خلال السؤال عن بعض الخصائص (attributes) فى الاقلام وليكن منهم نوع الحبر ولنعبر عنة بالمتغير X1,وقابليتة للمسح ونعبر عنة بالمتغير X2 فتجمع لدينا هذة المعلومات

نوع الحبر x1	قابليتة للمسح x2	التصنيف Classification Y
7	7	BAD
7	4	BAD
3	4	GOOD
1	4	GOOD

الان لدينا منتج جديد فى المصنع لقلم جديد ولة خاصيتين X1=3 , X2=7 هل يمكننا التنبؤ بتصنيف هذا القلم؟ لنتبع خطوات الخوارزمية:

1-نحدد قيمة للمتغير الذى سوف يعبر عن عدد المجاورين k وليكن قيمة k=3

2- نحسب قيمة المسافة بين المنتج الجديد والامثلة التى فى dataset ,فى مثالنا هذا سوف نعتمد على Euclidean Distance حيث يتم حساب المسافة بين نقطتين p,q من المعادلة:

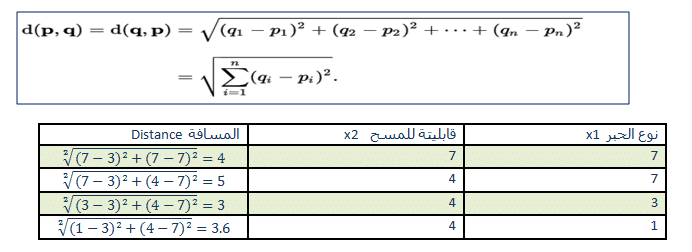
3- نرتب الامثلة لنحصل على المجاورين أعتمادا على أقل مسافة تم حسابها فى الخطوة السابقة ونأخذ منهم عدد k مجاور وحيث k هنا قيمتة 3 مجاورين فقط وبترتيب الامثلة حسب المسافة الاقل سوف نلغى المثال الثانى من ان يكون من المجاورين

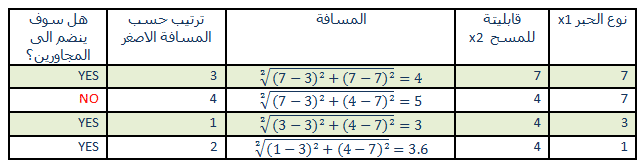
4-نحدد قيمة التصنيف للمجاورين كما فى العمود الاخير فى الجدول التالى

5- الكلاس الاكثر اغلبية للمجاورين هو GOOD حيث لدينا ثلاثة أمثلة اثنين منهم GOOD وواحد فقط BAD لذا الكلاس المتوقع لهذا القلم الجديد هو GOOD

الان أعتقد أن الخوارزمية بسيطة جدا لنطبق على أمثلة معقدة او مشاكل حقيقية من الحياة Real World Problem

~ The Iris dataset ~

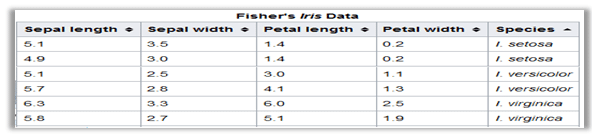
مجموعة البيانات زهرة Iris أو مجموعة البيانات Fisher’s Iris هى مجموعة من البيانات متعددة المتغيرات multivariate data set وسميت بهذا الاسم نسبة الى العالم رونالد فيشر الذى اعلن عنها فى بحثة سنة 1936, مجموعة البيانات Dataset عبارة عن 150 مثال(عينة) لثلاثة أنواع من زهرة Iris:

Iris setosa
Iris virginica
Iris versicolor

تم قياس أربع سمات او خصائص attributes or features من كل نوع: طول وعرض sepals وطول وعرض petals ,هذا جزء مستقطع من الـ Iris datasetلتوضيحها فى الجدول التالى:

المشكلة التي نريد حلها هي، “طبقا لمجموعة البيانات السابقة DataSet” اذا حصلنا على زهرة جديدة ، هل يمكننا التنبؤ بنوعها من قياساتها ؟

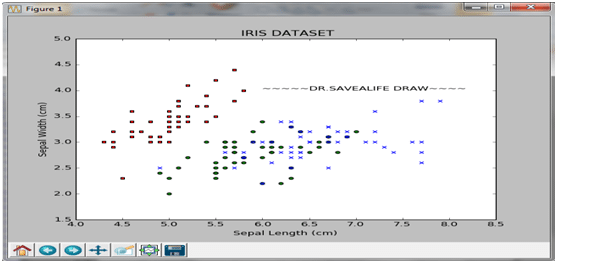
بداية هل نكتب كود لعمل رسم بيانى لهذة الdataset لان رؤية البيانات بشكل مرئى يعتبر خطوة أولية لفهم هذة المشكلة “Visualization is a good first step”

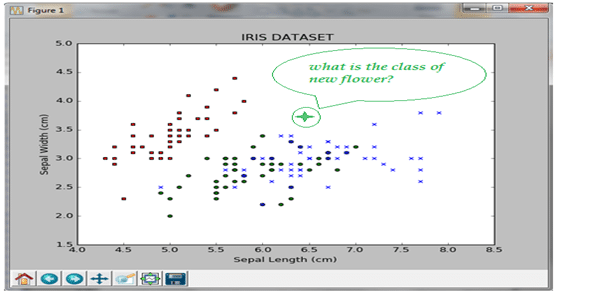
من الرسم البيانى نجد ان البيانات تنقسم الى مجموعتين كبيرتين :الاولى لزهرة Iris setosa والتى نرمز لها بالمربع الاحمر والمجموعة الثانية هى خليط من Iris virginica والتى نرمز لها بعلامة x الزرقاء و Iris versicolor بالدائرة الخضراء, الان اذا لدينا زهرة جديدة كما بالشكل التالى .هل يمكن تصنيفها ؟

المشكلة تعتبر مشكلة تصنيف Classification problem حيث لدينا مجموعة بيانات dataset تتكون من مجموعة أمثلة instances كل مثال لة كلاس معين هل نستطيع تصميم قاعدة rule بحيث تجعلنا نتنبأ بالكلاس لاى مثال جديد غير موجود فى dataset, مشكلة التصنيف لها تطبيقات كثيرة فى الحياة منها تصينف الرسائل هل هى من الرسائل المزعجة spam او ليست من الرسائل المزعجة not spam وغيرها من المشاكل التى سوف نتطرق لها بعد ذلك بأذن الله تعالى

~~~~ التطبيـــــق العمــــــلى بالكــــــــــــود~~~~~~

أولا :التصنيف بأستخدام خوارزمية k-nearest neighborمن الصفر

k-nearest neighbor from scratch

بعد تحميل ملف الـ iris dataset من الموقع:

https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data
1-الخطوة الاولى التعامل مع البيانات Handle Data:
نبدأ بقراءة الملف وتقسيم البيانات عشوائيا الى training set ,test set باستخدام الميثود loadDataset

import csv
import random
def loadDataset(filename, split, trainingSet=[] , testSet=[]):
with open(filename, 'rb') as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x][y])
if random.random() < split:
trainingSet.append(dataset[x])
else:
testSet.append(dataset[x])

يمكن تجربة الميثود بأستخدام الكود التالى:

trainingSet=[]
testSet=[]
loadDataset('iris.data', 0.66, trainingSet, testSet)
print 'Train: ' + repr(len(trainingSet))
print 'Test: ' + repr(len(testSet))

2-الخطوة الثانية إنشاء ميثود لحساب المسافة او التشابهة Similarity:
نكتب الميثود euclideanDistance تحسب المسافة بين اى مثاليين وقد تعرضنا من قبل للصيغة الرياضية لها

import math
def euclideanDistance(instance1, instance2, length):
distance = 0
for x in range(length):
distance += pow((instance1[x] - instance2[x]), 2)
return math.sqrt(distance)

3-الخطوة الثالثة ايجاد المجاورين Neighbors:
هذة الميثود سوف تستخدم الميثود euclideanDistance لايجاد المسافة بين المثال الجديد والtrainingset ثم ترتب الامثلة تنازليا من التى لها مسافة أصغر للحصول على المجاورين

import operator 
def getNeighbors(trainingSet, testInstance, k):
distances = []
length = len(testInstance)-1
for x in range(len(trainingSet)):
dist = euclideanDistance(testInstance, trainingSet[x], length)
distances.append((trainingSet[x], dist))
distances.sort(key=operator.itemgetter(1))
neighbors = []
for x in range(k):
neighbors.append(distances[x][0])
return neighbors

4-الخطوة الرابعة تحديد الmajority : بعد تحديد المجاورين للمثال الجديد الان نحدد الكلاس الذى لة اكثر اغلبية بينهم وهو النتيجة لتصنيف هذا المثال الجديد

import operator
def getResponse(neighbors):
classVotes = {}
for x in range(len(neighbors)):
response = neighbors[x][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
sortedVotes = sorted(classVotes.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedVotes[0][0]

5- حساب دقة الخوارزمية Accuracy:
فى هذة الخطوة نحسب كم عدد الامثلة التى تم التنبؤ بالكلاس الصحيح لها فى testSet

def getAccuracy(testSet, predictions):
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] is predictions[x]:
correct += 1
return (correct/float(len(testSet))) * 100.0

ثانيا :التصنيف بأستخدام مكتبة scikit-learn

Classifying with scikit-learn

فى السابق كتابنا كود لبرمجة خوارزمية knn من البداية ولكن لغة python لغة مناسبة جدا لتعلم machine learning لأنها تحتوى على العديد من المكتبات الممتازة وخاصة المكتبة scikit-learn وفى هذا الجزء سوف نتعلم استخدامها لعمل تصنيف للبيانات باستخدام خوارزمية knn بداية يجب أن تعلم أن scikit-learn classification API تعتمد على أثنين ميثود :

fit(features, labels)
predict(features)

الميثود fit وهى خطوة يتم فيها التعلم training من الامثلة التى لدينا
ثم نستخدم الميثود predict للتنبؤ بالكلاس لمثال جديد
الان لنبدأ بخطوات استخدام المكتبة scikit-learn :
1-الخطوة الاولى التعامل مع البيانات Loading the data:

بداية نعمل import لمجموعة البيانات dataset

# Import load_iris function from datasets module
from sklearn.datasets import load_iris

ثم نستخدم الميثود load_iris() لجلب dataset كلها ثم حفظها فى الكائن iris

# save object containing iris dataset and its attributes

iris = load_iris()

لجلب الامثلة instances نستخدم iris.data

# Store feature matrix in "features"
features = iris.data·

لجلب الكلاس لكل مثال نستخدم iris.target

# Store response vector in "target"
target = iris.target

لمعرفة ابعاد dataset نستخدم الامر shape

# prints the shapes of features and target
print features.shape

والنتيجة هى انة يوجد 150 مثال كل واحد يحتوى على اربع خصائص

 (150,4)

2-الخطوة الثانية : التعامل مع scikit-learn فى 4 خطوات:
1) قم بعمل import للكلاس الذى سوف تستخدمة فى عملية التصنيف وسوف نستخدم هنا خوارزمية knn لذا نكتب

from sklearn.neighbors import KNeighborsClassifier

2)قم بعمل كائن من Estimator وحدد عدد المجاورين

knn = KNeighborsClassifier(n_neighbors=1)

print knn

والنتيجة هى:

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=1, p=2,
weights='uniform')

3)اعطى الكائن الذى انشأتة knn البيانات والتى هى الامثلة والكلاس المتوقع لها

knn.fit(features, target)

4)استخدم الـ Estimatorللحصول على النتيجة اذا اعطيتة مثال جديد

knn.predict([[3, 5, 4, 2]])

النتيجة هى ان هذا المثال الجديد تم التنبؤ لة بالكلاس 2 وهى زهرة virginica array([2]))
array([2])
5)يمكن ان تعطية اكثر من مثال للحصول على نتيجة مرة واحدة

X_new = [[3, 5, 4, 2], [5, 4, 3, 2]]
knn.predict(X_new)

النتيجة هى ان هذا المثال الجديد الاول تم التنبؤ لة بالكلاس 2 وهى زهرة
Virginica والمثال الثانى تم التنبؤ لة بأنة من زهرة versicolor

array([2, 1])

~ The digits dataset~

هى عبارة عن مجموعة من البيانات تتكون من 1797 صورة وكل صورة عبارة عن مصفوفة 8X8 ، والصورة تمثل رقم ما كما هو موضح أدناه .

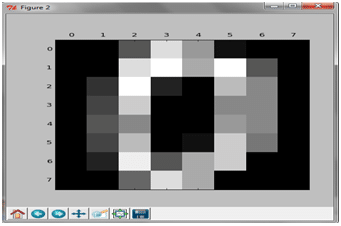
اذا هذة الdataset عبارة عن مجموعة من الامثلة كل مثال عبارة عن صورة من 8×8 وعدد الكلاسات 10 ولدينا تقريبا 180 مثال لكل كلاس والمجموع الكلى للامثلة هو 1797 وسوف نمثل الصورة بvector ابعادة 64 الخصائص تمثل بأرقام من” صفر الى 16″

Classes	10
Samples per class	~180
Samples total	1797
Dimensionality	64
Features	integers 0-16

لمزيد من المعلومات عن digits dataset

http://scikitlearn.org/stable/modules/generated/sklearn.datasets.load_digits.html#sklearn.datasets.load_digits

ما الذى تنتظرة الان لدينا dataset وفهمنا خصائصها لنستخدم مكتبة scikit-learn لعمل التصنيف classification

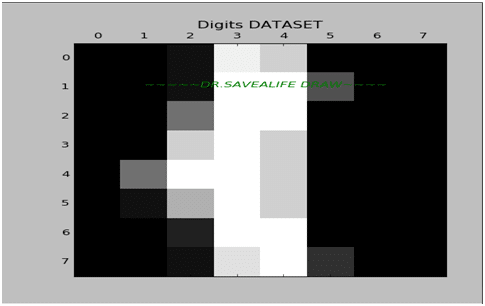
فى الكود السابق قمنا بالخطوات التى تعلمناها مسبقا عمل load الى dataset ثم قمنا بعمل تدريب training لهذة الdataset بخوارزمية knn حيث استخدامنا الميثود fit ثم اختبرنا البرنامج بمثال لصورة الذى ترتيبها رقم 99 باستخدام الميثود prdict ووجدنا انها اعطتنا تصنيف للكلاس الصحيح الان هل يمكنك التنبؤ عن الرقم الموجود فى هذة الصورة:

اذا لا تعرف الاجابة عند تطبيق الكود السابق فهذة الصورة تعبر عن الرقم “1”

ما هى عيوب هذة الخوارزمية

يجب علينا إختيار قيمة دقيقة لعدد المجاورين “Choosing the right value of k “لانة يمكن ونحن نحل احد المشاكل نجد المجاورين يكون الكلاس الذى لة اغلبية كبيرة اكثر من واحد فمثلا [‘blue’, ‘blue’, ‘red’, ‘red’]فكيف فى هذة الحالة نختار الكلاس الاكثر أغلبية؟

2-ان الخوارزمية تعتبر Lazy-learning اى انة لايتم تكوين قاعدة للتنبؤ إلا عند الاحتياج لمعرفة ما هو الكلاس لمثال جديد.

المراجع