سميت بهذا الإسم لأنها تفترض أن النتائج الغير معروفة يمكن تقديرها بالإعتماد على معادلة الخط المستقيم y=mx+b
لنفترض أن لدينا مجموعة بيانات ممثلة بهذا الجدول وهذا المخطط لأطوال ساق نبتة في عدة أيام مختلفة
| (طول ساق النبتة (سم |
اليوم |
| 0.5 | الأول |
| 0.9 | الثاني |
| 1.5 | الثالث |
| 2.3 | الخامس |
| 3 | السادس |
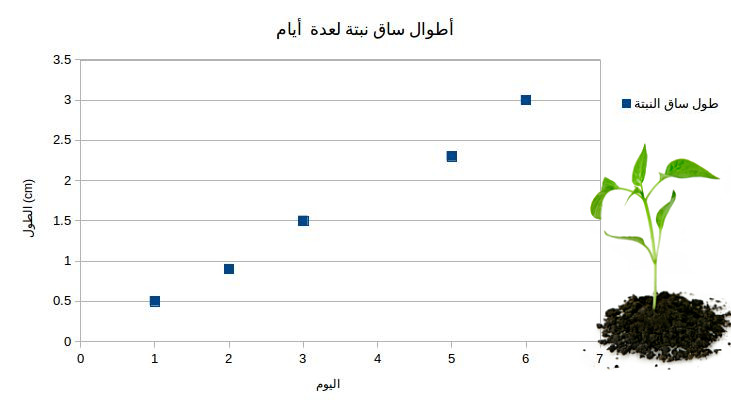
مخطط يوضح العلاقة بين الزمن و طول ساق النبتة
إذا أردنا مثلا أن نعرف طول ساق النبتة في اليوم الأول سنرى ما يقابلها في الجدول وهو 0.5 سنتيمتر، في اليوم الثاني كانت بطول 0.9 سنتمتر إذا العملية بسيطة جدا إذا توفر لدينا جدول لكل القيم التي نحتاجها وهذا لن نجده دائما فمثلا إذا أردنا أن نقدر طول ساق النبتة في اليوم الرابع لن نستطيع معرفة ذلك من الجدول مباشرة لكن باستخدام معادلة الخط المستقيم يمكننا تقدير ذلك إذا قمنا برسم خط مستقيم وحاولنا أن نجعله يمر بأكبر عدد ممكن من النقاط في عملية تسمى ملائمة خطية (linear fitting) هكذا

مخطط يوضح ملائمة الخط المستقيم للنقاط المبعثرة على المستوى
الآن نستطيع تقدير طول ساق النبتة في اليوم الرابع وذلك بالتعويض في معادلة هذا الخط المستقيم عن قيمة اليوم الرابع (الزمن) وحساب طول ساق النبتة أو من خلال الرسمة مباشرة سنرى بأنه يساوي 1.9 سنتيمتر تقريبا وهكذا أصبح بإمكاننا تقدير طول ساق النبتة في أي ساعة وفي أي لحظة باستمرار .
لاحظ أن ميل الخط المستقيم m ونقطة تقاطع الخط المستقيم مع المحور الرأسي b وكلما كانت قيمة m وb مضبوطتان بشكل صحيح كلما كانت القيم المقدرة أقرب إلى القيمة الحقيقية
لكن كيف سنقوم بملائمة الخط المستقيم على مجموعة من البيانات وتحديد الزاوية الأنسب للميل عن طريق برنامج يعمل على الحاسوب ؟
يلزمنا أولا أن نكتب دالة تقوم بحساب قيمة الخطأ للقيم المقدرة وفي كل مرة نقوم بتعديل زاوية الميل والإزاحة الرأسية حتى نصل إلى أقل قيمة خطأ ممكنة
الجواب بسيط لكن كيف سنحسب قيمة الخطأ إذا كانت النتائج الحقيقية مجهولة ؟!
نحن لدينا مجموعة بيانات معروفة مسبقا سنستخدمها للتدريب، في البداية ستكون زاوية الميل والإزاحة الرأسية قيم عشوائية ثم سنقوم بحساب النتائج في كل مرة بتقديرها عن طريق معادلة الخط المستقيم وسنقارنها بالنتائج المعروفة لدينا مسبقا من الجدول لنقوم بتصحيح الخطأ .
دالة حساب قيمة الخطأ لكل نقطة= القيمة الحقيقية – القيمة المقدرة
![]()
| a(x) | طول ساق النبتة الحقيقي في اليوم x |
| y(x) | طول ساق النبتة الذي تم تقديره بواسطة المعادلة y=mx+b |
لكن هذه الدالة ستقوم بحساب قيمة الخطأ لنقطة واحدة فقط يعني في كل يوم على حدة ونحن نريد أن تحسب قيمة الخطأ الكلي لجميع النقاط وهذا ممكن عن طريق هذه الدالة التي ستقوم بحساب قيمة الخطأ الكلي وهذه الدالة عادة يطلق عليها دالة الكلفة أو دالة الخطأ
من الواضح أن الدالة تقوم بحساب قيمة الخطأ لكل نقطة ثم تجمعها مع قيمة الخطأ للنقطة التي تليها ثم ستقسم الناتج على عدد النقاط لتحسب متوسط الخطأ ، يمكننا تفسير التربيع أيضا بأننا لا نريد قيم سالبة لكن لماذا ضربنا الناتج في ½ ?
هذا الثابث سيساعدنا على تبسيط المعادلة عندما نحتاج إلى تفاضل ما بين الأقواس المرفوعة للأس التربيعي سنستخدم قاعدة السلسلة ونضرب الناتج في الأس وهو في حالتنا هذه 2 ثم نختصر الإثنين في المقام والبسط لنتخلص من الثابت وهكذا تم تبسيط المعادلة
هذه الدالة ستمكننا من حساب قيمة الإنحراف الكلي للنقاط .
الآن بعد أن كتبنا معادلة نستطيع من خلالها تقدير قيمة الخطأ الكلي لتموضع الخط المستقيم على البيانات المبعثرة في المستوى (x,y)
سنحتاج طريقة ما لتصحيح ميل المستقيم وقيمة إزاحته الرأسية بناءا على قيمة الخطأ لهذا الغرض سنستخدم إحدى تقنيات التحسين (Optimization Techniques) وهي خوارزمية الإزاحة المتدحرجة أو gradient descent شائعة الإستخدام هذه التقنية تعتمد على مبدأ بسيط وهو السير بخطوات تكرارية في الإتجاه المعاكس لتدرج الدالة ولأن تدرج الدالة أو بمعنى آخر تفاضلها الجزئي دائما يكون في إتجاه أكبر معدل زيادة لها فإن الخطوات التي تسير عكس هذا الإتجاه ستقلص قيمة الدالة مع الوقت ، لا تقلق إذا لم تتضح الصورة جيدا تابع هذا الشرح
الإزاحة المتدحرجة أو gradient descent
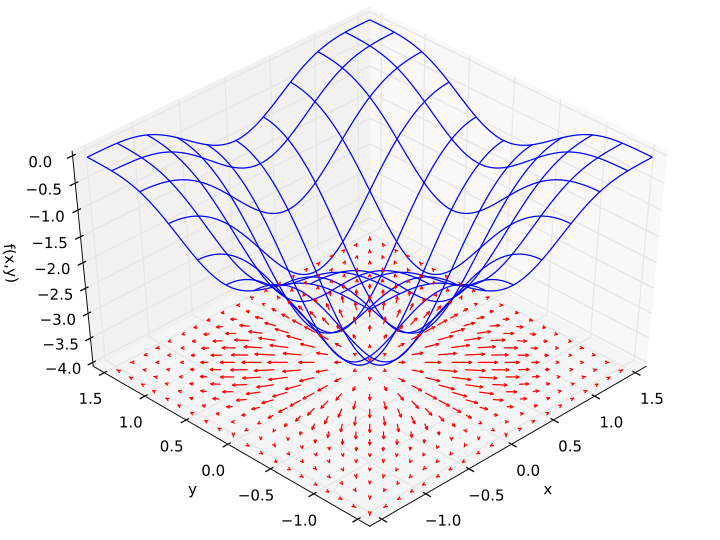
التدرج أو gradient هو تعميم التفاضل على الدوال متعددة المتغيرات، إذا كان بإمكانك تفاضل دالة في متغير واحد كذلك يمكنك حساب تدرج دالة في متغيرات متعددة وذلك باستخدام التفاضل الجزئي بالنسبة لمتغير واحد في كل مرة مثلا إذا كان لدينا دالة في متغيرات (x,y) موضحة باللون الأزرق في المخطط بالأسفل فنتيجة التدرج هي المتجهات الموضحة باللون الأحمر لاحظ أن اتجاه المتجهات يشير إلى أكبر معدل زيادة للدالة في كل نقطة وأن مقدارها يمثل الإنحناء slope هذا يعني أن المتجهات أكبر في الأماكن التي تزداد فيها قيمة الدالة بشكل أكبر ولذلك يعرف التدرج بأنه يشير دائما إلى أكبر معدل زيادة للدالة هذه الخاصية يمكننا الإستفادة منها في حالة أردنا العكس وهي القيم التي تنقص فيها قيمة الدالة وذلك بعكس الإتجاه!
وهذا هو التعبير الرياضي لخوارزمية الإزاحة المتدحرجة
![]()
الدالة F هي دالة الكلفة أو دالة الخطأ الرمز نبلا هو مؤثر التدرج على الدالة F يعني التفاضل الجزئي للدالة F بالنسبة للمتغير a
المتغير الذي نريد أن تتقلص قيمة الدالة عنده في الخطوة التالية a
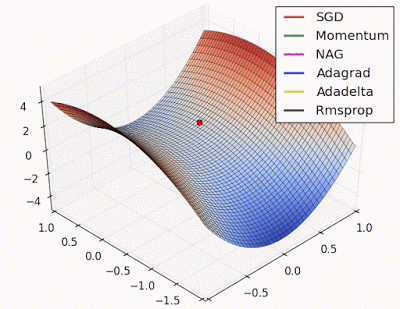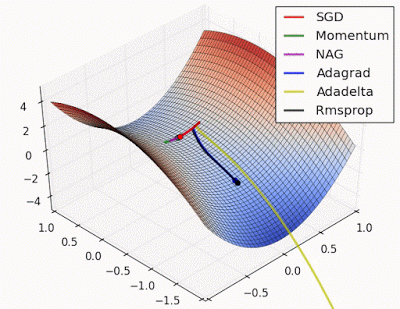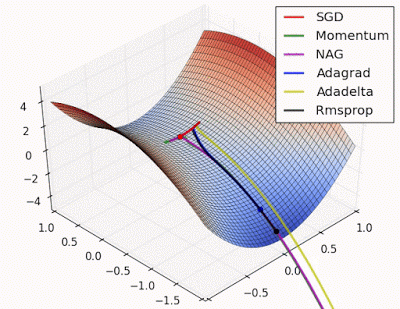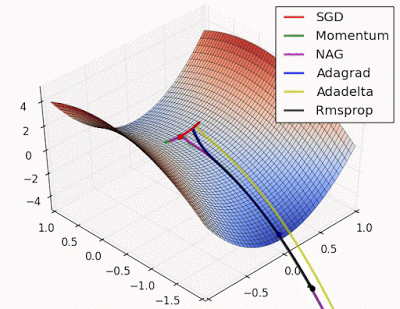
إذا قمنا برسم مخطط ثلاثي الأبعاد يبين قيمة الخطأ لكل قيم الميل والإزاحة المختلفة،دالة الخطأ ستشكل شكل مشابه لهذا الموجود بالأسفل، قيمة الخطأ الكلي على المحور z مقابل قيمة الميل m وقيمة الإزاحة الرأسية b وطبقنا خوارزمية الإزاحة المتدحرجة على المتغيرات m,b في كل مرة ستقل قيمة الخطأ وعندما تصل إلى أدنى مستوى نكون قد حققنا المطلوب، النقاط الظاهرة باللون البنفسجي تمثل تدحرج الدالة نحو القاع
هذه الصورة المتحركة توضح الفرق بين كفاءة عدة تقنيات تستخدم لتقليص قيمة الخطأ وهي مثالية لتوضيح طريقة عملها
الكرة الحمراء تمثل الطريقة التي نتحدث عنها وهي تقنية الإزاحة المتدحرجة Gradient Descent
للمزيد من التوضيح
إذا قمنا بتطبيق تقنية الإزاحة المتدحرجة على دالة الخطأ الكلي أو دالة الكلفة ستقوم الخوارزمية بالبحث عن أقل قيمة خطأ في كل خطوة وتنزاح إليها وذلك بتغيير القيم الإبتدائية لميل المستقيم وإزاحته على المحور الرأسي حتى تصل إلى أقل قيمة خطأ ممكنة كما هو موضح بالمسار البنفسجي على المخطط .
نعلم مما سبق الآن أن الإنحدار أو التدرج (gradient) يعني التفاضل الجزئي للدالة الذي سيعطينا ميل المماس هذا الميل يقع في اتجاه أكبر زيادة للدالة عند طرح هذه القيمة من قيمة المتغير الذي فاضلنا الدالة بالنسبة له سنحصل على قيمة متغير جديدة تتقلص قيمة الدالة عندها ، يمكننا التحكم في مقدار التدحرج عن طريق ثابت لمدا يجب اختياره بشكل مناسب حتى لا تبتعد الدالة كثيرا .
بعد تقليص قيمة الخطأ لدالة الكلفة ، يمكننا استخدام القيم الجديدة الناتجة من خوارزمية الإزاحة المتدحرجة ونعوض في معادلة الخط المستقيم
ولأن لدينا متغيران m و b سنطبق خوارزمية الإنحدار المتدرج مرتان
مرة للمتغير m الذي يمثل ميل الخط المستقيم

ومرة أخرى للمتغير b الذي يمثل نقطة تقاطع المستقيم مع المحور الرأسي
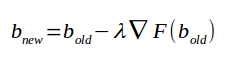
عند تكرار هذه الخطوات أكثر من مرة سنحصل على قيم m و b عند اقل قيمة خطأ ممكنة .
بعد تحديد أفضل قيمة ميل m وأفضل إزاحة رأسية b أثناء عملية التدريب على البيانات التي لدينا يمكننا كتابة معادلة الخط المستقيم بالقيم الجديدة وتقدير إرتفاع النبتة في أي لحظة بالتعويض في المتغير x وحساب y
ملخص الخطوات
أولا قمنا بتحديد معادلة رياضية لنستخدمها في تقدير النتائج هذه المعادلة في هذا المثال كانت معادلة الخط المستقيم يطلق على هذه المعادلة غالبا hypothisis أو افتراض هذا يعني أنه يمكننا كتابة
hypothisis = mx+b or h(x)=mx+b
ثانيا قمنا بكتابة معادلة الكلفة أو معادلة الخطأ التي استخدمناها في حساب قيمة الخطأ الكلي للنتائج المقدرة بواسطة معادلة الخط المستقيم
رابعا قمنا بتدريب نموذجنا المكون من معادلة تقدير نتائج ومعادلة حساب قيمة الخطأ حتى نحصل على أفضل نتائج للثوابت m و b وهما عادة يرمز لهم بالرمز 𝜽n… 2𝜽 1𝜽
خامسا استخدمنا نموذجنا الذي تم تدريبه في تقدير أطوال ساق النبتة في أوقات غير مدونة في الجدول .
هذه النقاط الأساسية سنكررها دائما لكن بطرق مختلفة مع كل خوارزميات التدريب المختلفة .
ملاحظات
ربما تلاحظ أن معادلة الخط المستقيم ستعطي قيم غير معقولة إذا قدرنا طول ساق النبتة بعد زمن طويل فقد تتوقف عن النمو بعد مدة معينة ، في الواقع هي ليست المشكلة الوحيدة التي ستواجهنا فطول ساق النبتة لا ينمو بشكل خطي أصلا وقد تختلف سرعة النمو من نبتة إلى أخرى و هذه المشاكل ستواجهها في كل تطبيقات وخوارزميات تعلم الآلة لذلك لا يجب أن تتوقع أن نماذجنا مثالية فهي يمكنها تقدير نتائج قريبة جدا وعملية لكنها قد تخطيء وتعطي نتائج غير صحيحة لذلك يوجد عدة اجراءات لتقليل نسبة الخطأ قدر الإمكان
الإعتماد على مجموعة كبيرة من بيانات التدريب في حالتنا هذه لا يجب الإعتماد على قراءة واحدة لنبتة واحدة ربما نحتاج إلى العشرات منها أيضا لا تتوقع بأنه كلما زادت بيانات التدريب ستزيد الدقة لأنك ستصل إلى مرحلة ستسقر عندها قيمة الخطأ!
وضع قيود على البيانات فمثلا في مثالنا هذا ربما نضع شرط لنتأكد من أن الزمن لا يتعدى عشرة أيام أو حتى أسبوع
التحجيم عادة يوجد تباين أو اختلاف كبير بين عينات أو بيانات التدريب مع أنها أخذت من حقل واحد ، مثلا كانت لدينا أطوال ساق نبتة في طرف المزرعة وأخرى قريبة من مصدر مياه سيكون هناك اختلاف في سرعة النمو عادة تستخدم علاقات تناسب للتعامل مع شريحة كبيرة من البيانات
استخدام فرضية مختلفة (hypothesis) ببساطة إذا كانت هذه الطريقة غير دقيقة استخدم طرق أخرى أكثر دقة فمثلا يمكنك استخدام معادلات غير خطية متعددة الحدود من الدرجة الثانية أو الثالثة أو الرابعة لتجعل المنحنى يتموضع على النقاط بشكل أفضل



comparer les prix génériques kamagra
kamagra achat en ligne sans ordonnance livraison rapide
donde comprar enclomiphene en lima
cheap enclomiphene generic canada
how to order androxal buy japan
cheapest buy androxal lowest cost pharmacy
does flexeril cyclobenzaprine really work
buy flexeril cyclobenzaprine purchase in the uk
comprar dutasteride original
online order dutasteride generic tablets
canadian womens gabapentin vs united states gabapentin
get gabapentin cheap uk buy purchase
fildena xr buy online cheap
buy cheap fildena canada purchase
ordering itraconazole canada internet
order itraconazole cheap in uk
purchase avodart purchase uk
buying avodart canada on sale
buying staxyn generic uk buy
cheap staxyn purchase to canada
order rifaximin cheap next day delivery
buy cheap rifaximin generic uae
Overnight xifaxan without a perscription
purchase xifaxan generic now
kupte si kamagra online bez souhlasu dr
kamagra recepty
Yo, j9app! Just checked it out. Pretty slick interface, and the game selection is seriously impressive. Definitely worth a look if you’re hunting for a new spot. Check it out here: j9app
Anyone used aaajililogin? Thinking of giving it a try, but curious about the community feedback. Let me know your thoughts! aaajililogin
Onebravip! Sounds VIP, are the perks legit? Lets go! Hope the experience lives up to the name. Have some fun here: onebravip
PPCine traz entretenimento completo no seu dispositivo. Faça o ppcine download, use PPCine APK e desfrute de PP Cinema com cinema apk atualizado e streaming fluido.