خوارزمية البحث الخطي Linear search

السلام عليكم و رحمة الله و بركاته

هذه المقالة تابعة لسلسلة خوارزميات البحث و الترتيب و التي ستأتيكم بقية حلقاتها تباعا و كلي أمل بأن يستفيد الجميع.

مقدمة :

تُعتبر خوارزمية البحث ركنا أساسيا من أركان علم الخوارزميات و تتخذ هذه الخوارزمية عدة أشكال, من أبسطها البحث عن عدد في مصفوفة مُحددة الحجم و يزداد الأمر تعقيدا عند الانتقال إلى البحث عن كلمة داخل نص, تماما كما ترى في محررات النصوص العادية والتي تحتوي على خاصية Find & Replace حيث أن أغلب المحررات الحالية تستخدم خوارزميه بحث تسمى Boyer-Moore Searching التي تُعد تقريبا من أسرع الخوارزميات في مجال البحث. هناك أيضا بحث من نوع آخر, فماذا لو كانت لدينا مجموعة حروف و نريد إيجاد جميع الكلمات التي تبدأ بهذه الحروف ؟؟ عادة ما يُسمى هذا النوع من الخوارزميات بــ prefix searching و لهذا النوع تطبيقات كثيرة خصوصا في محركات البحث و القواميس و المتصفحات التي تستخدم هذه الخوارزمية عند كتابتك لموقع يبدأ بحرف كنت قد زرته سابقا.
لا تقتصر خوارزمية البحث على ما ذكرناه آنفا, فهناك نوع آخر من الخوارزميات يُستخدم لإيجاد نص قريب من النص الذي كنت تبحث عنه, حيث تقوم الخوارزمية بالبحث عن 4 أو 5 كلمات قريبة من الكلمات الخاطئة, تماما كما يفعل Google عند الترجمة أو Office Word عند كتابة نص يحتوي على أخطاء إملائية و تعتمد أغلب هذه الخوارزميات على الوزن الصوتي للحرف و من أشهرها Soundex Searching.
ليس هذا فقط، فمضادات الفيروسات تستخدم خوارزميات بحث سريعة للبحث عن وجود توقيع مطابق لأحد بيانات الملف المراد فحصه، وبما أن قواعد بيانات التواقيع تكون ضخمة للغاية فالبحث عن كل توقيع سيكون بطيئا جدا وهناك الأفضل، حيث توجد خوارزميات بإمكانها البحث عن عده تواقيع في نفس اللحظة وتستخدم بنية شجرية للقيام بهذا الأمر، هناك أيضا خوارزميات أخرى تعتمد على مفاهيم مختلفة مثل Hash Table وعدة أمور أخرى، و يُسمى هذا النوع من الخوارزميات بـ Multiple pattern searching و هو من أصعب الخوارزميات، وهناك العديد من مضادات الفيروسات التي تستخدم مثل هذه الخوارزميات مثل ClamAV.

في هذا الدرس سنتكلم عن أبسط هذه الخوارزميات وهي خوارزمية البحث الخطي أو Linear search algorithm. بعدها سنتكلم عن خوارزميات الترتيب و بعدها سننتقل إلى خوارزمية البحث الثنائي Binary search algorithm إن شاء الله.

في هذه المقالة سنتطرق إلى النقاط التالية :
1. الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات)
2. الخوارزمية بلغة السي++.
3. التعقيد الزمني.
4. ملأ مصفوفة عشوائيا و اختبار سرعة الخوارزمية.
5. كم تحتاج هذه الخوارزمية من الوقت لتنفيذ مهمتها ؟
6. اختبر قدراتك !

1. الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات)

الهدف : البحث عن قيمة المفتاح key داخل المصفوفة X.
الفكرة : تعتمد هذه الخوارزمية على البحث التسلسلي (Sequential Search) في المصفوفة X حيث يبدأ البحث من أول عنصر إلى أن تنتهي المصفوفة, و في كل مرة نقارن محتوى الخانة الحالية X[i]l مع المفتاح Key, فإذا كانت القيمتان متساويتان (X[i] = Key) ستتم إعادة قيمة المتغير i الذي يُمثل مكان وجود المفتاح Key في المصفوفة X, أما إذا كانت القيمتان مختلفتان فسننتقل إلى الخانة الموالية X[i+1]l للبحث من جديد و هكذا.
النتيجة : إذا كان Key موجود في X فسنحصل على رقم الخانة التي يوجد بها المفتاح و إلا فالقيمة المـُعادة ستكون -1.
الإيجابيات : الخوارزمية بسيطة و تقليدية أيضا كما لا يُشترط الترتيب عند البحث.
السلبيات : بطيئة و غير عملية, خصوصا عند معالجة المصفوفات الضخمة.

2. الخوارزمية بلغة السي++

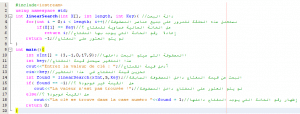
الدالة linearSearch تستقبل 3 وسائط, الأول هو اسم المصفوفة المراد البحث داخلها و الوسيط الثاني هو طول المصفوفة أما الوسيط الثالث فهو المفتاح الذي نبحث عنه. بكل بساطة قمنا باستخدام حلقة for للمرور على جميع عناصر المصفوفة (لاحظ أن البحث خطي) واضعين بذلك شرط الحلقة كما يلي : إذا كانت قيمة الخانة الحالية مُساوية لقيمة المفتاح فقم بإعادة رقم الخانة. (مفهوم إعادة القيمة يرتبط بالخروج من الدالة)
طيب ماذا عن الحالة العكسية ؟ أقصد إذا كان المفتاح غير موجود في المصفوفة ؟ هنا تأتي فائدة إعادة -1. يُمكنك إبدال -1 بأي عدد سالب تماما, المهم أن لا يكون موجبا أو معدوما حتى لا يقع التباس بين القيمة التي تدل على عدم وجود المفتاح و رقم الخانة التي يوجد بها الأخير.
نأتي الآن إلى الدالة الرئيسية main :

في البداية قمنا بالإعلان عن مصفوفة باسم xInt عدد عناصرها 5 ثم قمنا أيضا بالإعلان عن متغير باسم key حيث طلبنا من المستخدم إدخال قيمة للمتغير. لننتقل إلى الجزء الأهم في الــ main و هو تطبيق الدالة linearSearch على المصفوفة xInt و المتغير key :
تم الإعلان عن متغير جديد باسم found الذي يحوي القيمة المـُعادة من طرف الدالة. بعد ذلك قمنا بفحص قيمة found فإذا كانت قيمته مساوية لــ -1 فهذا يعني أن المفتاح غير موجود في المصفوفة و إلا فالمفتاح موجود في الخانة رقم found+1 لأن الترقيم يبدأ من صفر فالخانة رقم 0 هي الخانة الأولى و هكذا.

تحذير : الوسيط الثاني للدالة يُمثل الطول الفعلي للمصفوفة لذا لا تحاول أن تُرسل إلى الدالة عدد أكبر من طول المصفوفة لأن هذا الفعل يؤدي إلى حدوث الــ buffer overflow الذي ينتج عنه انتهاك لتسيير الذاكرة و قد يتوقف برنامجك. يمكنك إرسال عدد أصغر من طول المصفوفة إذا كنت ترغب في أن يقتصر البحث على جزء من المصفوفة.
ملاحظة : إذا وُجد المفتاح أكثر من مرة في المصفوفة X فإن الدالة ستعيد رقم أول خانة يظهر فيها المفتاح.عليك الآن بتغيير الدالة لتعيد رقم آخر خانة يُوجد بها المفتاح.

إضافة بسيطة :
ماذا لو أردنا معرفة عدد المرات التي ظهر فيها المفتاح داخل المصفوفة ؟ لنفترض أن المصفوفة كبيرة جدا و سيتم البحث داخل مصفوفة جزئية من المصفوفة الرئيسية. إذا كل ما سنقوم به هو إضافة متغير جديد إلى جسم الدالة (أو لنقل عداد) و زيادة هذا العداد كلما وجدنا خانة مساوية للمفتاح هكذا :

في هذه الحالة ستستقبل الدالة أربع وسائط هي : اسم المصفوفة الجزئية و من أين تبدأ و أين تنتهي ؟ إضافة إلى المفتاح.
كالعادة نبدأ بالمرور على جميع عناصر المصفوفة و كل ما وجدنا خانة مُساوية للمفتاح أضفنا 1 إلى قيمة العداد. عند نهاية الحلقة, إذا كانت قيمة العداد أكبر أو تساوي واحد فإن المفتاح يوجد على الأقل مرة واحدة داخل المصفوفة و هنا ستتم إعادة قيمة المتغير found و في حالة العكس ستتم إعادة -1.

في الدالة الرئيسية قمنا بالإعلان عن مصفوفة تحتوي على 18 عنصر بينما قمنا بالبحث عن القيمة 17 داخل مصفوفة جزئية تتكون من 6 عناصر فقط (المصفوفة الجزئية تبدأ من الخانة السادسة و حتى الثانية عشر). برأيك ما مُخرجات البرنامج ؟

3.التعقيد الزمني :
كما ذكرنا آنفا فإن هذه الخوارزمية تعتمد على البحث الخطي أو المتسلسل حيث يبدأ البحث من أول خانة منتقلا إلى الخانة المجاورة إن لم يجد المفتاح و هكذا حتى الوصول إلى الخانة الأخيرة. مما يعني أن الزمن المستغرق لتنفيذ هذه الخوارزمية يزيد كلما زاد حجم المصفوفة. إذا خوارزمية البحث الخطي لها تعقيد زمني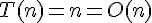
في أفضل الحالات يمكن أن نجد المفتاح في أول خانة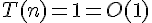
و في المتوسط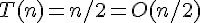
و في أسوء الحالات يمكن أن نجد المفتاح في الخانة الأخيرة كما يمكن أن يكون هذا الأخير غير موجود.

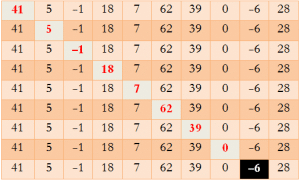
كمثال للتوضيح لنفترض الجدول الآتي :

إذا قمنا بتطبيق خوارزمية البحث الخطي على الجدول فسنمر بالخطوات التالية :

يوجد المفتاح في الخانة ذات اللون الأبيض و الخلفية السوداء و في كل مرة تتم مقارنة الخانة ذات اللون الأحمر و الخلفية البيضاء مع المفتاح. لاحظ أنه من خلال البحث عن المفتاح تم تشكيل قطر لمثلث قاعدته عبارة عن المصفوفة التي تبدأ بأول عنصر و تنتهي بالمفتاح.

4. ملأ مصفوفة عشوائيا و اختبار سرعة الخوارزمية

قمت بإدراج هذه الفقرة لكي ألفت انتباهك أخي القارئ إلى مفهوم التعقيد الزمني من الناحية العملية. لذا سنقوم بالإعلان عن مصفوفة (كبيرة الحجم نسبيا) تحتوي على مائة ألف خانة ثم نقوم بملأ هذه المصفوفة بشكل عشوائي و من ثم نستدعي دالة البحث للبحث عن المفتاح.
بكل بساطة, توجد حالتان, إما أن يكون المفتاح غير موجود داخل المصفوفة أو العكس. الحالة الأولى ثُمثل أسوأ حالات الخوارزمية أما الحالة الثانية فقد تمثل أفضل الحالات أو الحالة المتوسطة. ما يهمنا في هذه الفقرة هو عدد الخانات التي مرت بها الدالة قبل الوصول إلى المفتاح أو لنقل عدد المقارنات اللازمة للحصول على الخانة المساوية لقيمة المفتاح.
إذا لم يتم العثور على المفتاح فهذا يعني أن عدد المقارنات يساوي عدد عناصر المصفوفة أما إذا تم العثور على المفتاح فهذا يعني أن عدد المقارنات يساوي رقم الخانة التي يوجد بها المفتاح + 1 لأن ترقيم عناصر المصفوفة يبدأ من صفر.

ملاحظة :

• تكرار الأعداد العشوائية المـــُولدة يعتمد على عدة عوامل منها سعة المجال الذي تم توليد الأعداد العشوائية بداخله.
• سبق و أن كتبتُ موضوع يتحدث عن توليد الأعداد العشوائية بشيء من التفصيل في منتديات الفريق العربي للبرمجة, يمكنك مراجعة الموضوع من هنا :
  توليد الأرقام العشوائية ! (نظرة تحليلية مفصلة)

5. كم تحتاج هذه الخوارزمية من الوقت لتنفيذ مهمتها ؟

قد يدور في ذهنك السؤال التالي :
هل نستطيع رصد الوقت الذي تستغرقه هذه الخوارزمية ؟ و الإجابة هي نعم فهناك دوال API تمكننا من الحصول على فترات توقيت أقل من 1 ميلي ثانية، لكن ولسوء الحظ فإن هذه الدوال تعتمد بشكل كامل على النظام و خصوصا المعالج المركزي. يجب أن يدعم النظام ما يسمى بــ عداد الأداء عالي الدقة (High Resolution Performance Counter) حيث تعتمد دقة هذا العداد على المعالج المركزي.

توجد دالتان من دوال API تستخدمان لهذا الغرض :
الدالة الأولى هي QueryPerformanceFrequency حيث تعطينا تردد العداد أو لنقل عدد الدورات في الثانية الواحدة و تعيد صفراً إذا كان النظام لا يدعم العداد العالي الدقة. أما الدالة الثانية فهي QueryPerformanceCounter التي تعيد القيمة الحالية للعداد.
بهذا يمكننا تقييم المدة التي يأخذها تنفيذ جزء معين من الكود و ذلك باستدعاء الدالة QueryPerformanceCounter مباشرة قبل الجزء الذي نريد تقييم مدته الزمنية ثم استدعائها مرة أخرى مباشرة بعده، ثم نحسب الفرق و نقسمه على التردد فنحصل على الوقت الذي استغرقه تنفيذ ذلك الجزء من الكود.
نفرض مثلاً أن التردد كان 50000 دورة في الثانية، و أن القيمة التي حصلنا عليها قبل الكود هي 1500 و القيمة بعد الكود هي 3500, الفرق هو 2000، و بالقسمة على 50000 نحصل على 0.04 ثانية.

يمكنك أيضا استخدام timeGetTime أو GetTickCount إذا أردت معرفة التوقيت بدقة أقل. يمكنك بهذه الإجراءات قياس الفروق الزمنية بدقة ميللي ثانية واحدة على الأكثر، وهذه الدقة قد تكون كافية لقياس عمل الخوارزمية التي نتحدث عنها. بهذه الطريقة ستريح نفسك من الصداع الذي تسببه لك المؤقتات الأخرى مثل QPC و RDTSC.

المؤقت QPC يستخدم ما يحلو له في الجهاز ليقدم أكبر دقة ممكنة. قد يعتمد في بعض الأجهزة على تعليمات مباشرة للـــ BIOS ، وفي بعض الحالات قد يقرأ القيم من أماكن أخرى غريبة. لذا ليست له وحدة ثابتة تستطيع استخدامها، فعندما تنادي الدالة
QueryPerformanceCounter ستستقبل قيمة .. الله أعلم ماذا تعني !! قد تكون الدورة هي معدل نبض ساعة المعالج Processor Clock وقد تعني أي شيء آخر. لذلك أنت بحاجة إلى شيء ما يساعدك على تحويل هذه القيمة إلى وحدة زمنية كالثواني, وهنا تأتي الإجراء فائدة الدالة QueryPerformenceFrequency حيث تعيد عدد “الوحدات” في الثانية الواحدة. (انظر Timing ومشاكله !)

مثلاً : أعطتنا QueryPerformanceFrequency القيمة 15000000 (15 مليون وحدة في الثانية)، وسنسميها التردد. وقمنا باستدعاء QueryPerformanceCounter مرتين على فترتين متباعدتين وطرحنا الفرق لنحصل على 45000000.
الآن يمكننا أن نقسم هذه القيمة على التردد لنحصل على 3 ثواني. وهذا هو مبدأ عمل المؤقت QPC الذي تصل دقته إلى النانوثانية، ويستخدم في تزمين الصوت مع الصورة في مشغلات الأفلام كما يُستخدم في قياس الزمن المستغرق لتنفيذ الإجراءات السريعة في ++C.
إلا أن هناك بعض الأمور التي تمنع QPC من أن يكون مؤقتاً مثاليا, تتخلص هذه الأمور في شيئين : تعدد المعالجات، والمعالجات التي تغير سرعتها بشكل مستمر.
في حالة تعدد المعالجات، لو اعتمد QPC على عداد التعليمات في المعالج (وهي الحالة الأكثر شيوعاً) فإنك قد تحصل على نتائج غريبة بين النداءات المختلفة للإجراء، وذلك بحسب أي المعالجات قام بتنفيذ الطلب. فمثلاً المعالج الأول أنجز مئة مليون تعليمة حتى الآن، بينما الثاني أنجز 90 مليون تعليمة فقط، ولذلك فقد تحصل أحياناً على نتائج مضحكة ! كأن يعود الزمن إلى الوراء ( يكون الفرق سالبا ) أو يقفز قفزات كبيرة مفاجئة للأمام.
في الحالة الثانية فإن بعض المعالجات تغير سرعتها بشكل مستمر على حسب الطاقة المتوفرة، وهذه المعالجات تتواجد بشكل رئيسي في الأجهزة المحمولة laptops حيث يخفف المعالج من سرعته عندما يدخل في نظام توفير طاقة البطارية.. وهنا فإن قيمة التردد التي حسبناها مسبقاً تصبح خاطئة لأن التردد قد تغير ويجب قراءته مرة أخرى …!

6.اختبر قدراتك :

لدينا مؤسسة صغيرة تحتوي على مجموعة من العمال, كل عامل مُعرف برقم ID واسم و مرتب الشهر, عند تشغيل البرنامج سيُدخل المستخدم اسم العامل و كلمة المرور ثم يقوم البرنامج بالبحث داخل بيانات العمال, فإذا كان اسم العامل موجود و كلمة المرور صحيحة فسيتم إظهار رسالة ترحيبية بالإضافة إلى المرتب الشهري للعامل و إلا فسيُظهر البرنامج رسالة تفيد بأن هذا العامل غير مُسجل.

إلى هنا أصل بكم إلى نهاية الدرس, أرجو أن تكونوا قد استفدتم. لا تنسوني من صالح الدعاء.
تحياتي.