السلام عليكم و رحمة الله و بركاته
تحدثنا في الحلقة الأولى عن خوارزمية البحث الخطي و في الحلقة الثانية عن خوارزمية ترتيب الفقاعات و سنتحدث في هذه المقالة عن خوارزمية البجث الثنائي.
في هذا الدرس سنتطرق إلى النقاط التالية :
- الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات)
- الخوارزمية بلغة السي++
- أمثلة على الخوارزمية
- التعقيد الزمني.
- ملأ مصفوفة عشوائيا و اختبار سرعة الخوارزمية.
- اختبر قدراتك !
1. الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات)
الهدف : البحث عن قيمة المفتاح key داخل المصفوفة X.
الفكرة : تعتمد هذه الخوارزمية على البحث الثنائي (Binary search) في المصفوفة X حيث يبدأ البحث من العنصر الذي يقع في وسط المصفوفة, و في كل مرة نقارنه مع المفتاح Key, إذا كانت القيمتان متساويتان, فهذا يدل على أنه تم إيجاد قيمة المفتاح في المصفوفة, أما إذا كانت القيمتان مختلفتان ستقوم الخوارزمية بإجراء فحص جديد, إذا كانت قيمة المفتاح أصغر من قيمة العنصر الأوسط سيتم البحث في الجزء الأيسر من المصفوفة و في الحالة المعاكسة سيتم البحث في الجزء الأيمن من المصفوفة, و هكذا .. حتى نحصل على مصفوفة تتكون من خانة واحدة قيمتها مساوية للمفتاح أو مختلفة عنه.
النتيجة : إذا كانت X تحتوي على Key فسنحصل على رقم الخانة التي يوجد بها الأخير و إلا فالقيمة المـُعادة ستكون -1.
الإيجابيات: الـ Binary search تُنصف (تقلص للنصف) عدد عناصر المصفوفة في كل تكرار, لذا تستغرق عملية البحث وقت قليل جدا.
تنتمي هذه الخوارزمية إلى عائلة فرق تسد.
السلبيات : خوارزمية البحث الثنائي أكثر تعقيدا من خوارزمية البحث الخطي التقليدية, كما أن الأولى تشترط الترتيب عند البحث.
2. الخوارزمية بلغة السي++
يمكننا كتابة الخوارزمية باستخدام الـ While loop أو الـ Recursive Function.
2.1 – الطريقة الأولى:
الدالة binarySearch تستقبل 3 وسائط, المصفوفة المـُراد البحث داخلها و عدد عناصرها و قيمة المفتاح.
يبدأ ترقيم عناصر المصفوفة بالقيمة low و ينتهي عند high, ويمثل المتغير mid رقم الخانة الوسطى من المصفوفة.
في كل مرة نقارن قيمة المفتاح بقيمة أوسط عناصر المصفوفة, إذا كانتا متساويتين نُعيد رقم الخانة و إذا كانتا مختلفتين نتقدم خطوة إلى الأمام أو نرجع خطوة إلى الوراء حسب وضعية المفتاح.
نكرر الخطوات السابقة ما دام low أقل أو يساوي high (بمعنى آخر, المصفوفة تحتوي على خانة أو أكثر).
إذا تم الخروج من الحلقة while دون إعادة قيمة فهذا يعني أن المفتاح غير موجود, في هذه الحالة ستعيد الدالة -1.
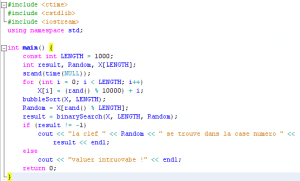
في الدالة الرئيسية قمنا بالإعلان عن مصفوفة تحوي ألف عنصر ثم ملأناها بالقيم الواقعة في المجال [500,500-] لاحظ أن عناصر المصفوفة يجب أن تكون مرتبة. بعد ذلك قمنا بالبحث عن القيمة -73 داخل المصفوفة و قد تم إيجادها في الخانة رقم 427 وهذا شيء طبيعي لأن الصفر يتواجد في الخانة رقم 500 و بالتالي القيمة -73 ستتواجد في الخانة رقم 73-500.
يمكننا استدعاء الدالة binarySearch على جزء من المصفوفة, في هذه الحالة نضع low و high كوسائط للدالة و ليس كمتغيرات محلية.
2.2 – الطريقة الثانية:
تستقبل الدالة binarySearch أربع وسائط, هم على التوالي : اسم المصفوفة و المفتاح و من أين يبدأ البحث ؟ و أين ينتهي ؟
المتغير mid يحتوي على رقم الخانة الوسطى من المصفوفة. إذا كانت قيمة المفتاح أكبر (أصغر) من mid سيتم تطبيق الدالة على الجانب الأيسر (الأيمن) من المصفوفة.
إذا كانت قيمة high أقل تماما من low فهذا يعني أن المصفوفة أصبحت فارغة.
3. أمثلة على الخوارزمية
نبدأ مع مثال بسيط يُوضح فكرة البحث الثنائي.
3.1 – المثال الأول
أحمد: ما رأيك بلعبة الكاهن ؟
عمرو: الكاهن ؟؟
أحمد: نعم, أختارُ عددا عشوائيا يقع في المجال [0,100] و عليك معرفة العدد !
عمرو: هذا مستحيل !!
أحمد: لا تستعجل .. في كل مرة تختار فيها عددا, سأخبرك ما إذا كان أكبر أو أصغر من العدد الذي تبحث عنه.
عمرو: لا بأس, سأحاول .. سأبدأ بالعدد الذي يقع في منتصف المجال, هل عددك أكبر من 50 ؟
أحمد: نعم !
عمرو : سأختار الآن أوسط أعداد المجال الجديد, هل العدد أكبر من 75 ؟
أحمد: لا !
عمرو: إذا العدد يقع بين 51 و 75, هل هو أكبر من 63 ؟
أحمد: نعم !
عمرو: جيد, أصبح المجال ضيقا الآن, هل العدد أصغر من 69 ؟
أحمد : نعم !
عمرو: أكبر من 66 ؟
أحمد: لا !
عمرو: أصغر من 65 ؟
أحمد: لا !
عمرو: إذا فالعدد المُختار هو 66 ؟
أحمد: نعم, أحسنت !
ملاحظة:
- لو وضع عمرو في الحسبان أن العدد الذي يبحث عنه يمكن أن يتواجد في منتصف المجال, لاستغنى عن آخر سؤالين !
- للفائدة, سبق و أن كتبتُ موضوعا في الفريق العربي للبرمجة يحتوي برنامجا صغيرا يُحاكي لعبة الكاهن, يمكنك تجربته من هنا.
3.2 – المثال الثاني
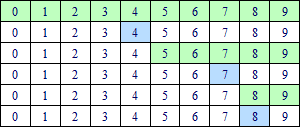
نريد البحث عن العدد 8 في مصفوفة مُكونة من 10 خانات, قيمها كالآتي:
الخانات الملونة باللون الأخضر تُمثل الجزء الذي سيتم البحث فيه من المصفوفة و الخانة ذات اللون الأزرق تمثل أوسط العناصر.
3.3 – المثال الثالث
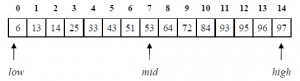
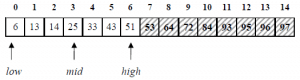
ابحث عن القيمة 33 في المصفوفة التالية :
الحل:
1. نحدد منتصف المصفوفة:
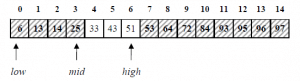
2. تقسيم المصفوفة إلى قسمين وفقا لموقع mid:
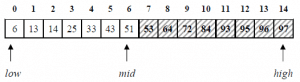
3. بما أن 33 أصغر من 53, فعملية البحث ستنفذ على النصف الأول:
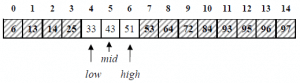
4. نعيد عملة التقسيم على النصف الأول و تصبح قيمة mid تساوي:
5. بما أن 33 أكبر من 25, سيتم استبعاد النصف الأول و تستمر عملية البحث في النصف الثاني:
6. من جديد, نعيد عملية التقسيم حيث تصبح قيمة mid تساوي 5:
7. و أخيرا نجد أن القيمة 33 موجودة في الموقع low و الذي يساوي 4.
4. التعقيد الزمني
خوارزمية البحث الثنائي سريعة جدا و فعالة أيضا, خصوصا عند التعامل مع المصفوفات الكبيرة, لأنها تُلغي في كل مرة نصف المصفوفة و تبحث في النصف الآخر (طبعا, دون أن ننسى أن المصفوفة يجب أن تكون مُرتبة و هذه ضريبة السرعة ![]() )
)
لو أخذنا على سبيل المثال مصفوفة تتكون من 1024 خانة, في أسوأ الحالات ستقوم الخوارزمية بـــ 10 مقارنات لمعرفة ما إذا كان المفتاح موجود أم لا ! (لاحظ أن 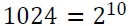
في أفضل الحالات, يكون التعقيد الزمني T(n) = 1 و في أسوأ الحالات يكون المفتاح في بداية أو نهاية المصفوفة أو غير موجود
في كل مرة يتم إلغاء نصف المصفوفة و العمل على النصف الآخر, لذا سيكون طول المصفوفة يساوي 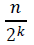
نتوقف عندما تصبح المصفوفة عبارة عن خانة واحدة:
إذا, في هذه الحالة سيكون التعقيد يساوي 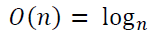
الحالة المتوسطة: عندما تكون هناك احتمالية وجود المفتاح في أي جزء من المصفوفة, و عليه سيكون التعقيد:
5. ملأ مصفوفة عشوائيا و اختبار السرعة
في هذه الفقرة, سنملأ عشوائيا مصفوفة تحتوي على 1000 خانة ثم نرتب المصفوفة لنبحث في داخلها عن قيمة معينة, سنحتاج إلى الدوال التالية لتنفيذ ما سبق:
لا شيء جديد, فقط قمتُ بتجميع الدوال التي تعرفنا عليها سابقا !
محتوى الدالة الرئيسية سيكون هكذا:
قمنا بملأ المصفوفة عشوائيا ثم رتبنا القيم تصاعديا, بعد ذلك قمنا بتخزين قيمة إحدى خانات المصفوفة في المتغير Random بشكل عشوائي ثم بحثنا عن مكان تلك القيمة داخل المصفوفة X. لاحظ سرعة الخوارزمية مُقارنة مع خوارزمية البحث الخطي التي تعرفنا عليها في الدرس الأول.
6. اختبر قدراتك !
هذه المرة احببت وضع تمرين محلول يكون بمثابة مراجعة للحلقات الثلاثة السابقة.
لتكن M مصفوفة ثنائية البعد, عدد صفوفها L وعدد أعمدتها C. المصفوفة مُرتبة تصاعديا حسب الأعمدة و حسب الصفوف أيضا.
- اكتب دالة تبحث داخل M عن قيمة معينة (تستقبلها كوسيط) ثم تُعيد true إذا كانت القيمة موجودة و false في الحالة المعاكسة.
- أعط التعقيد الزمني للدالة السابقة بدلالة L و C ؟
الحل :
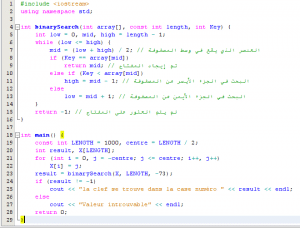
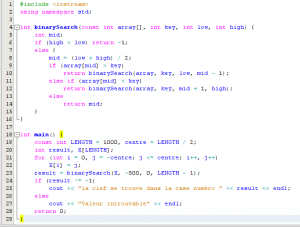
لإيجاد مكان المفتاح في المصفوفة, نبحث عن رقم السطر الذي يحوي قيمة المفتاح ثم نُطبق عليه خوارزمية البحث الثنائي, مع الأخذ في الاعتبار أن المصفوفة مُرتبة حسب الأعمدة و الصفوف أيضا:
#include <iostream>
using namespace std;
#define numberOfColumns 4
bool searchTwoDimensional(int array[][numberOfColumns], int rows, int columns, int value) {
int i = 0;
while (i <= rows - 1 && array[i++][0] <= value);
if (i == 0) return false;
else {
i--;
int low = 0, high = columns - 1, mid = (low + high) / 2;
while (array[i][mid] != value && low <= high) {
array[i][mid] < value ? low = mid + 1 : high = mid - 1;
mid = (high + low) / 2;
}
if (high < low) return false;
else return true;
}
}
int main() {
int newArray[3][numberOfColumns] = {
{1, 3, 5, 7},
{10, 15, 27, 28},
{30, 39, 52, 100}
};
cout << searchTwoDimensional(newArray, 3, numberOfColumns, 52);
return 0;
}
بعد الخروج من الحلقة الأولى, لدينا ثلاث حالات:
- i=0 و هذا يعني أنه لم يتم الدخول إلى الحلقة ! لأن قيمة أول عنصر في المصفوفة أكبر تماما من قيمة المفتاح. و بما أن المصفوفة مرتبة حسب الأعمدة و الصفوف, فيمكننا القول بأن المفتاح غير موجود في المصفوفة. في هذه الحالة ستعيد الدالة false.
- i أكبر أو يساوي 2 و أقل أو يساوي rows, في هذه الحالة سيمثل i رقم أول سطر يبدأ بقيمة أكبر تماما من قيمة المفتاح, لذا فإن المفتاح سيتواجد في السطر رقم i-1.
- i = rows + 1, هذه الحالة تعني أن جميع الأسطر تبدأ بقيمة أكبر تماما من قيمة المفتاح , قد يتواجد المفتاح في السطر الأخير من المصفوفة.
بعد الخروج من الحلقة الأولى (في حالة i يختلف عن الصفر), سيتنقل التنفيذ إلى الجزء المخصص للبحث عن قيمة المفتاح باستخدام خوارزمية البحث الثنائي. (راجع الحلقة السابقة إن لم تفهم هذا الجزء)
في الدالة الرئيسية, قمنا بالإعلان عن مصفوفة ثنائية البعد, تحتوي على 3 أسطر و أربعة أعمدة. ثم قمنا بالبحث عن القيمة 52 التي تتواجد في آخر أسطر المصفوفة.
بالنسبة للتعقيد الزمني :
في أسوأ الحالات, ستمر الحلقة الأولى على جميع أسطر المصفوفة و بالتالي سيكون تعقيدها الزمني من النوع 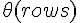
الحلقة الثانية لها تعقيد لوغاريتمي 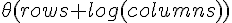
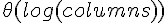
لا يمكننا تبسبط هذه العبارة لأننا لا نعرف العلاقة ما بين rows و columns.
تحياتي.




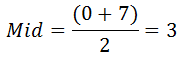
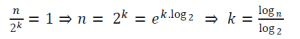
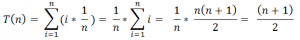



السلام عليكم
لو سمحت نحن محتاجين مثال ل binary search
اريد المثال بالغه الانجليزي ومعه الحل في java.
buy androxal purchase from canada
discount androxal purchase line
get enclomiphene cost on prescription
buy cheap enclomiphene generic cheap
online order rifaximin usa suppliers
cheapest buy rifaximin generic when available
online order xifaxan purchase online uk
buy xifaxan uk in store
purchase staxyn buy for cheap
how to buy staxyn how to purchase viagra
how to order avodart retail price
avodart prices walmart
discount flexeril cyclobenzaprine cheap online canada
order flexeril cyclobenzaprine cost usa
buy dutasteride purchase in canada
discount dutasteride real price
generic gabapentin online best
discount gabapentin generic germany
buy fildena online get prescription
cheap fildena generic effectiveness
indianpharmaonline itraconazole
india prescription drugs itraconazole
kamagra dodání ve stejný den
kamagra online objednávka bez lékařského předpisu
generique kamagra remede tarif en pharmacie
phizer brand kamagra made in usa
Just signed up to nh88com. Site’s alright, pretty standard stuff. Haven’t won big yet, but I’ve had some decent runs. Kinda wish their bonus terms were clearer, but overall it’s a passable place to gamble. Check it out if you’re bored: nh88com.
Trying to find the main Bong88 site? Trangchubong88 might be the place. Gimme the real deal, baby! trangchubong88
trangchubong88 … I think it’s a Bong88 homepage in another language. Anyone know if navigation is easy enough without knowing the language? trangchubong88
8xvn is a new one for me. Checking it out and it seems to have a lot to offer. The interface is intuitive. So far, its nice site 8xvn.
Yo, lucky777app, you’ve been keepin’ me entertained! Easy to use and the games are actually pretty fun. Check it out lucky777app.
777phslot, slots are fun, and the graphics are pretty good. I’ve had a few wins, so I can’t complain. Spin those reels at 777phslot.