السلام عليكم و رحمة الله و بركاته
تحدثنا في الجزء الأول من هذه السلسلة عن خوارزمية البحث الخطي و كان من المفترض أن نتحدث في هذه المقالة عن خوارزمية الترتيب الثنائي و لكن أحببت أن أبدأ بإحدى خوارزميات الترتيب نظرا لأن الـــ Binary search algorithm يعتمد على فكرة الترتيب. في هذه المقالة (أو لنقل بقية حلقات السلسلة) ستجدني أتحدث أحيانا مع شخص افتراضي اسمه عمرو, ألجأ إلى الحديث مع هذا الشخص عندما أصل إلى فقرة تحتاج إلى توضيح أكثر.
في هذا الدرس سنتطرق إلى النقاط التالية :
- الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات)
- قبل أن نبدأ .. إليك 4 طرق لعمل Swap
- كتابة دالة تقوم بعملية التبديل
- الخوارزمية بلغة السي++
- التعقيد الزمني.
- ملأ مصفوفة عشوائيا و اختبار سرعة الخوارزمية.
1. الخوارزمية (الهدف, الفكرة, النتيجة, الإيجابيات و السلبيات) :
الهدف : ترتيب عناصر المصفوفة X تصاعديا أو تنازليا. (في بقية الدرس سنعتبر أن الترتيب تصاعدي و n هو عدد عناصر المصفوفة X)
الفكرة : تقارن هذه الخوارزمية بين قيم الخانات المتجاورة, تبدأ بالمقارنة بين أول خانتين من المصفوفة, إذا كان محتوى الخانة الأولى أكبر من محتوى الخانة الثانية سيتم تبادل محتوى الخانتين و هكذا مع بقية الخانات. عند انتهاء الدورة الأولى ستكون الخوارزمية قد أنجزت n-1 مقارنة و بهذا ستتم إزاحة أكبر عناصر المصفوفة إلى الخانة الأخيرة. بقي الآن ترتيب الــ n-1 عنصر. و هكذا الأمر مع بقية الدورات …
النتيجة : عملية الترتيب تـخـتلف عن عملية البحث في هذه النقطة, فالترتيب لا يقبل وجود عدة احتمالات في النتيجة, فعند تطبيق الخوارزمية سنحصل على مصفوفة مرتبة تصاعديا و بالتالي لا توجد احتمالات للمناقشة.
الإيجابيات : الخوارزمية سهلة التصور و بسيطة المفهوم.
السلبيات : بطيئة شيئا ما وغير عملية, خصوصا عند معالجة المصفوفات الضخمة.
2. قبل أن نبدأ .. إليك 4 طرق لعمل Swap :
من خلال دراستك لخوارزميات الترتيب المختلفة ستجد أن مفهوم Swap أو تبادل مُحتوى متغيرين يتكرر باستمرار .. فأغلب خوارزميات الترتيب (إن لم تكن كلها !) تعتمد في مرحلة ما على تبديل محتوى خانتين لوضعهما في الترتيب الصحيح, لذا سنوضح كيفية تبديل محتوى متغيرين قبل أن نبدأ بكتابة الخوارزمية بلغة السي++.
سنتناول فيما يلي 4 طرق لعمل Swap, لكل منها إيجابيات كما لها سلبيات أيضا.
الطريقة الأولى (و هي الأكثر شهرة) تكمن في استخدام وسيط مساعد يُساعدنا على تبديل محتوى المتغيرين, فنضع قيمة المتغير الأول في الوسيط ثم نضع قيمة المتغير الثاني في المتغير الأول ثم نضع قيمة الوسيط في المتغير الثاني, و بهذا نكون قد بادلنا بين قيمة المتغير الأول و الثاني. لنفرض أن x=5 و y=-1 :
t = x //t = 5 x = y //x = -1 y = t //y = 5
في النهاية تكون x=-1 و y=5 . و بالتالي تم تبديل قيمتي x و y.
يمكنك تـخيل الفكرة كما يلي .. لدينا كأسين x و y, الكأس x يحتوي على العصير و الكأس y يحتوي على الماء, لو أردنا أن نُبادل محتوى الكأسين, (أي نجعل الماء في الكأس x و العصير في الكأس y) سنقوم باستخدام كأس ثالث فارغ (وهو الوسيط المساعد t) و تكون عملية التبادل كما يلي :
- نجعل العصير في الكأس الفارغ.
- نجعل الماء في الكأس x.
- نجعل العصير في الكأس y.
الآن أصبح الكأس x يحتوي على الماء و الكأس y يحتوي على العصير. هذه الطريقة بسيطة و تقليدية أيضا, إلا أنها تأخذ مساحة أكثر من الذاكرة بالإعلان عن الوسيط الثالث.
يمكننا عمل Swap بدون حاجة إلى وسيط مساعد عن طريق إجراء بعض العمليات الحسابية البسيطة على المتغيرين.
الطريقة الثانية (تصلح للمتغيرات العددية فقط) :
x=x+y; y=x-y; x=x-y;
الطريقة الثالثة (تصلح للمتغيرات العددية فقط و يجب أن تختلف قيمة y عن الصفر) :
x=x*y; y=x/y; x=x/y;
ملاحظة : الطريقتان السابقتان يمكنهما أن يتسببا في حدوث Overflow إذا كانت قيمة x+y أو x*y أكبر من القيمة العظمى لنوع المتغيرين x,y.
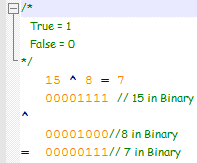
توجد أيضا طريقة رابعة لا تحتاج إلى وسيط مساعد و لا يمكن أيضا أن تكون سببا في حدوث Overflow. تعتمد هذه الطريقة على أحد الــ Bitwise (مؤثرات الــ Bit) وهو المؤثر XOR (اختصار لـــ Exclusive OR) و الذي يُرمز له بــ ^ , هذا المؤثر يعطينا True إذا و فقط إذا كان المدخلين مختلفين, أما إذا كانا متشابهين فالنتيجة ستكون False و يعمل هذا المؤثر كالتالي :
و كمثال على ذلك :
سنقوم بتجربة هذه الطريقة على المتغيرين x و y حيث x = 15 و y=7, لذلك سنقوم بالخطوات الثلاثة التالية :
x = x^y // x = 15 XOR 7 = 8 y = x^y//y = 8 XOR 15 = 7 x = x^y//x = 7 XOR 8 = 15
و بهذا تم تبديل محتوى المتغيرين x و y.
يمكننا الآن كتابة دالة تبادل بين مُحتوى مُتغيرين باستخدام إحدى الطرق الأربعة الموضحة أعلاه, مع الأخذ في الاعتبار سلبيات كل طريقة.
إذا أدرت التوسع أكثر في هذه الجزئية, فيمكنك البحث عن أفضل طريقة لتبديل محتوى متغيرين بحيث تحقق النقاط الآتية في آن واحد :
- لا تحتاج إلى وسيط مساعد. (المستوى : بسيط)
- لا تسبب Overflow. (المستوى : صعيب)
- لا تضع أي شرط على قيم أو نوع المتغيرين. ( المستوى : أكثر صعوبة, إن لم يكن مستحيلا !)
3. كتابة دالة تقوم بعملية التبديل :
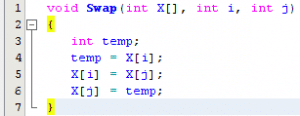
بعد أن تطرقنا إلى الطرق الأربعة التي يمكننا من خلالها تبديل محتوى متغيرين. سنقوم الآن بكتابة دالة تُبادل بين محتوى خانتين من المصفوفة X باستخدام الطريقة الأولى (لأنها الأكثر شعبية .. رغم احتوائها على انتهاك صارخ لحقوق الــ Overflow !) :
عمرو :لم أفهم استخدام المؤشرات !
أحمد : لا بأس !, سترتاح قليلا عندما تعلم أن الكتابة السابقة مُطابقة تماما للكتابة الآتية :
عمرو : كيف !؟
أحمد : الدالة السابقة تستقبل 3 وسائط, الأول عبارة عن اسم المصفوفة و الوسيطين, الثاني و الثالث عبارة عن أرقام الخانات الـمُراد تبديلها.
عمرو : لكن .. لماذا تُعيد الدالة void ؟
أحمد : ببساطة .. لأن هدف الدالة يكمن في تبديل محتوى الخانتين, فقط ! لا أكثر و لا أقل, لذا ليست هناك قيمة مُعادة. أغلب الدوال التي تستقبل “بالمرجع” تعيد void لأن التغيير سيحصل في المتغير نفسه. لذا لسنا بحاجة إلى إعادة قيمة المتغير الجديدة.
عمرو : طيب, لكنني لم أفهم الطريقة التي تستخدم المؤشرات !
أحمد : هل فهمتَ الطريقة الثانية ؟
عمرو : نعم
أحمد : إذا أنت بالتأكيد قد فهمت الطريقة الأولى !, دعني أسألك !
عمرو : تفضل
أحمد : ألم نقل أن الدالة Swap تستقبل مصفوفة ؟
عمرو : بلى !
أحمد : و هل المصفوفة عبارة عن كتلة واحدة ؟
عمرو : عفوا, لم أفهم السؤال !
أحمد : …كنت أقصد, هل تُـخَزَّن المصفوفة في خانة واحدة من الذاكرة ؟ كما يحدث مع الأنواع البدائية لللغة كــ int مثلا ؟
عمرو : لا! طبعا, فالمصفوفة عبارة عن مجموعة من الخانات المتجاورة فيما بينها و ليست خانة واحدة.
أحمد : جميل جدا, إذا .. كيف تستقبل الدالة هذه الخانات في آن واحد و تميزها عن غيرها ؟
عمرو: بصراحة .. لا أدري !
أحمد : الأمر بسيط جدا .. كما قلت أنت بنفسك قبل قليل ” المصفوفة عبارة عن مجموعة من الخانات المتجاورة فيما بينها ” و لكي يكون الكلام أكثر دقة يمكننا القول بأن المصفوفة عبارة عن مجموعة من العناصر المتجانسة(من نفس النوع) مُسجلة تحت اسم واحد ,حيث يمكن تمييز كل عنصر بترتيبه (دليله) في المصفوفة.
عمرو : …متجانسة ؟!
أحمد : نعم, متجانسة ! و إلا فسنحصل على structure أو class …عموما, دعنا في الموضوع !, قل لي .. كيف تُفرق بين مصفوفتين ؟
عمرو : بالإسم طبعا .. لأنه لا يمكن وجود أكثر من مصفوفة بنفس الإسم !
أحمد : طيب, لكن اسم المصفوفة ما هو إلا مؤشر يشير إلى أول عنصر فيها.
عمرو : أمممممم .. يبدو أن مفتاح الفكرة يكمن في العنصر الأول !
أحمد : بالضبط, فانطلاقا من العنصر الأول يمكننا الوصول إلى بقية عناصر المصفوفة عن طريق إزاحة المؤشر إلى الأمام, لأننا قلنا سابقا أن خانات المصفوفة مُتجاورة !
عمرو: و ماذا لو حصلنا على مصفوفة خاناتها غير مُتجاورة ؟
أحمد: مُستحيل .. المصفوفة بالتعريف هي مجموعة من الخانات المُتجاورة فيـــ…
عمرو: نعم .. نعم !, تذكرت ! …طيب, هل لك أن تُلخص لي فكرة الكود السابق ؟ فأفكاري حوله لم تنضج بعد !
أحمد: الدالة Swap تستقبل مؤشر من نوع int بالإضافة إلى رقمان يدلان على مكان وجود القيم التي نريد إبدالها فيما بينها. واضح ؟
عمرو: مفهوم !
أحمد: في جسم الدالة قمنا باستخدام وسيط مساعد من شأنه مُساعدتنا في عملية Swap. الكتابة *(X + i) يمكننا قراءتها “قم بإزاحة المؤشر i إلى الخانة الموالية” و بالتالي سيشير المؤشر إلى الخانة رقم i+1 لأن الترقيم يبدأ من صفر. بنفس الطريقة قمنا بإزاحة المؤشر للحصول على محتوى الخانة رقم j.و بهذا تمت عملية التبادل.
عمرو: اتضحت الفكرة. طيب, هل من تطبيق لما سبق ذكره ؟
أحمد: على مهلك, جواب سؤالك سيكون في الفقرة الموالية : )
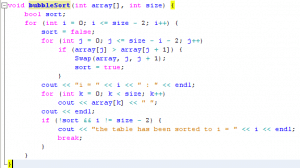
4. الخوارزمية بلغة السي++ :
كما ذكرنا سابقا فإن هذه الخوارزمية تقوم في الدورة الأولى بإزاحة أكبر عناصر المصفوفة إلى الخانة الأخيرة ثم تقوم في الدورة الثانية بإزاحة العدد الذي يلي أكبر العناصر إلى الخانة القبل الأخيرة و هكذا .. آخر دورة سيتم فيها وضع أصغر العناصر في الخانة الأولى. كل دورة ينتج عنها بعض التبديلات بين خانات المصفوفة مما يُساعد على تحسين ترتيب المصفوفة.
تستقبل الدالة bubbleSort وسيطين: اسم المصفوفة و عدد عناصرها. تبدأ الحلقة الأولى ذات العداد i من أول خانة في المصفوفة و حتى الخانة القبل الأخيرة.
عمرو : هل أفهم من كلامك أن الترتيب لن يشمل الخانة الأخيرة ؟
أحمد : كلا, لكن إذا وصل عداد الحلقة الأولى إلى القيمة size-1 سيؤدي هذا إلى حصول Underflow !, ستفهم أكثر بعد قليل … هناك حلقة ثانية, تبدأ في كل مرة من الخانة الأولى و حتى الخانة رقم size – i – 2.
عمرو : .. size – i – 2 !!؟, من أين أتيت بهذا العدد ؟؟
أحمد : الحلقة الثانية تعمل على ترتيب المصفوفة و في أسوأ الأحوال سيتم وضع عنصر واحد في الترتيب الصحيح. منطقيا .. إذا عادت الخوارزمية من جديد للترتيب فيجب أن تستثني العناصر التي تم ترتيبها. من أجل i=0 سيتم وضع أكبر الأعداد في الخانة الأخيرة (حصلنا على خانة واحدة مرتبة) و من أجل i=1 سيتم وضع العدد الذي يلي أكبر الأعداد في الخانة القبل أخيرة (حصلنا على خانتين مرتبتين). إذا في كل مرة سنحصل على size-i-1 من العناصر الغير مرتبة.
عمرو : و بعد ؟
أحمد: حتى لا نُعيد اختراع العجلة .. لكي يتم ترتيب العناصر الغير مرتبة فقط يجب أن تبدأ الحلقة الثانية من الخانة الأولى (رقم صفر) و تتوقف عند الخانة رقم size-i-1.. و لكي لا يحدث Overflow يجب أن يكون j+1 = size-i-1 مما يعني أن j=size-i-2 و هي القيمة التي تتوقف عندها الحلقة الثانية.
أحمد :نعود الآن إلى قضية الــ Underflow, عدد عناصر المصفوفة يساوي size, إذا رقم الخانة الأخيرة هو size-1 و رقم الخانة القبل أخيرة هو size-2, لاحظ أنه إذا كانت i=size-2 ستصبح j=0 وهنا ستتم مقارنة قيمة الخانة الأولى مع الثانية و إبدال محتوى الخانتين إذا كان الترتيب معكوسا و هذه هي آخر خطوات الخوارزمية.
أما إذا كانت i=size-1 فستصبح j=-1 و هذا خطأ منطقي لأن ترقيم المصفوفات يبدأ من صفر.
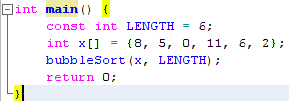
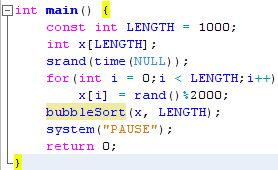
نأتي الآن إلى كتابة كود متكامل يحتوي على الدالة bubbleSort :
المتغير LENGTH يمثل طول المصفوفة x. قمنا بطباعة عناصر المصفوفة قبل و بعد استدعاء دالة الترتيب. لاحظ الفرق.
مثال للتوضيح :
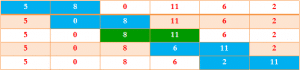
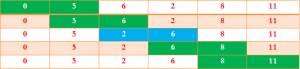
لنفترض أننا نريد ترتيب الجدول التالي :
عند تطبيق الخوارزمية على الجدول سنحصل على النتائج التالية :
إذا كانت i=0 :
في كل مرة يتم تبديل محتوى الخانتين ذوات اللون الأزرق الفاتح, الخانة ذات اللون الأخضر تدل على أن ترتيب الخانتين في الوضع الصحيح لذا لم تتم مبادلتهما. لاحظ أنه من خلال الدورة الأولى تمت إزاحة أكبر عناصر الجدول إلى الخانة الأخيرة (في هذا المثال تمت إزاحة العدد 11 إلى الخانة الأخيرة).
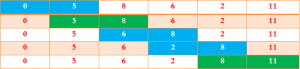
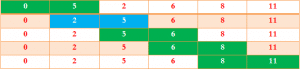
i=1 :
إذا كانت i = 1 فإن القيمة العظمى لــ j ستكون 3 و بالتالي لن تتم المقارنة بين محتوى الخانة الأخيرة و الخانة الموجودة قبلها. لاحظ أنه سيتم ترتيب عناصر الجدول انطلاقا من نهايته.
i = 2 :
إذا كانت i=2 فإن Jmax=2 و هذا يعني أن الخانات رقم 3,4,5 مُرتبة بشكل صحيح.
i = 3 :
لاحظ معي أنه تم ترتيب عناصر الجدول مع أن الحلقة لم تنتهي بعد فما زالت دورتان i=4, i=5.
ما رأيك لو أضفنا شرطا بسيطا يتعلق بالخروج من الدالة إذا وصلت الخوارزمية إلى ترتيب الجدول قبل انتهاء الحلقة ؟
إضافة بسيطة :
الفكرة ببساطة تكمن في استخدام متغير منطقي وتغيير قيمته عندما يتم تبادل محتوى خانتين. عندما نجد أنه لم تتغير قيمة المتغير منطقي في إحدى الدورات فهذا يعني أن خانات الجدول أصحبت مُرتبة بشكل صحيح.
مُحتوى الدالة الرئيسية سيكون هذا :
5. التعقيد الزمني :
تُعد خوارزمية ترتيب الفقاعات من أبطئ خوارزميات الترتيب حيث يعود السبب إلى كثرة عمليات المقارنة و التبديل. من أجل ترتيب جدول يحتوي على n عنصر سنحتاج إلى n-1 مقارنة (الأول و الثاني, الثاني و الثالث, … , ما قبل الأخير والأخير) ثم نكرر نفس العملية من جديد على جدول يحتوي على n-1 عنصر و هكذا دواليك. إذا المرور رقم i سيحوي n-i مقارنة و بالتالي سيكون التعقيد الزمني للخوارزمية من حيث عدد المقارنات يُساوي :
بالنسبة لعدد التبديلات : في أسوأ الحالات سنحتاج إلى n-i في المرور رقم i. في هذه الحالة نقول أن الجدول مُرتب بشكل مقلوب.
إذا نـخلص إلى أنه في المرور رقم i سنحتاج بالضبط إلى n-i مقارنة و n-i تبديل في أسوأ الحالات.
في أسوأ الحالات سيكون تعقيد الخوارزمية يساوي : 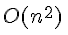
و في المتوسط سيكون عدد التبديلات يُساوي : 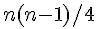
أما في أفضل الحالات فسيكون التعقيد خطيا : 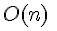
6. ملأ مصفوفة عشوائيا و اختبار سرعة الخوارزمية :
سبق و أن تعرضنا في الحلقة السابقة إلى ملأ مصفوفة عشوائيا, الجديد هنا هو استخدام عداد و زيادته كل ما تمت عملية تبديل, لا أكثر :
عند استدعاء الدالة bubbleSort سيتم إظهار عدد المرات التي تمت فيها عملية التبديل بالإضافة طبعا إلى رقم المرور الذي تمت فيه عملية الترتيب.
ملأ المصفوفة x عشوائيا و استدعاء الدالة bubbleSort داخل main سيكون هكذا :
إلى هنا أصل بكم إلى نهاية الدرس, أرجو أن تكونوا قد استفدتم. لا تنسوني من صالح الدعاء.
تحياتي.






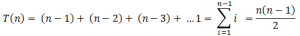



أبطأ خوارزمية ترتيب في العالم 🙂
احتاج رقمك او ايميلك استاذ اححمد ضروري ياليت تضعه لي هنا ??يعطيك العافيه ع الشرح
استاذ احمد ادرس هالمادة واواجه به صعوبه بصراحه قدحملتها قبل كذا وجد مهتمه منها??
how to order androxal uk suppliers
ordering androxal generic ingredients
buy cheap enclomiphene no prescription overnight delivery
get enclomiphene generic uk next day delivery
cheap rifaximin generic united states
ordering rifaximin generic in united states
online order xifaxan australia where to buy
buying xifaxan purchase in the uk
price staxyn
online order staxyn price in us
cheapest buy avodart generic online canada
buy cheap avodart purchase online safely
pas de script kamagra
kamagra navire canada phar
order dutasteride generic does it work
get dutasteride generic health
how to buy flexeril cyclobenzaprine generic usa
discount flexeril cyclobenzaprine generic europe
get gabapentin canada purchase
online order gabapentin usa buy online
cheap fildena purchase usa
order fildena generic canada no prescription
Buy itraconazole next day overnight fedex delivery order itraconazole cod
buy cheap itraconazole buy online usa
kamagra austrálie legální koupit online
fedex dodání kamagra
Gotta say, nh888 is growing on me. The user interface is actually pretty clean, and I haven’t had any issues with lag or glitches. They’ve got a good selection of slots. Definitely worth a shout if you’re looking for a new place to spin: nh888.
Thinking of signing up for V9Bet? Dangkyv9bet should have the registration details. Let’s see what they offer! dangkyv9bet
Alright fellas, heard good things about mv9bet. Anyone tried them out yet? Thinking about putting some bets down. Fingers crossed it’s legit! Check it out here: mv9bet
Alright, folks, finally checked out x89app! It’s got a decent selection, but could use some more variety, yeah? Give x89app a look see.
Hey all, just tried out jljl30login and it’s pretty straightforward to use. Logged in easy enough. Check it out for a quick go jljl30login.
So, I gave 567jililogin a shot. No complaints about the login process. It works as expected! Worth a peek 567jililogin.