الخوارزميات الجينية Genetic Algorithm

السلام عليكم ورحمة الله وبركاتة

تتناول المقالة بأذن الله شرح للخوارزميات الجينية:
تاريخها
مبدأها
الخوارزمية
اساسها
تطبيق على مشكلة من مشاكل الحياة
وضع الكود اللازم لكل جزء ::ان شاء الله::

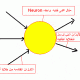
~تاريخها History

الgenetic algorithm تم اخترعها بواسطة جون هولند John Holland عام 1960وطورها هو وطلابة وزملائه وكانت فكرة الخوارزمية مبينة على نظرية التطور لداروين وما فيها من عملية الانتخاب الطبيعى

~مبدأ الخوارزمية ( البقاء للاصلح او الاقوى )

 

~قصة صغيرة من عالم العيش فى الغابة

كان لدينا مجموعة من الارانب سريعة وذكية واخرى بطيئة وغبية وكان الجيل الاول من الارانب يعيش بسعادة وامان حتى اتت مجموعة من الثعالب لتأكلة وفى هذة الحاله للاسف لم ينجو الا كثير من الارانب السريعة وقد نجت بعض الارانب البطيئة نتيجة الحظ ثم عاش الجيل المتبقى بعد ذلك الهجوم الشديد مع بعضهم فى امان وتم التزاوج بين هذة الارانب المتبقية والتى سوف تنقسم الى:    تزاوج ارانب سريعة مع اخرى مثلها–وارانب بطيئة مع سريعة–وبطيئة مع بطيئة

ومعنى ذلك ان الجيل الناتج سوف يأخذ جينات من الاباء والامهات ونتج جيل جديد ولكن استمرت هجوم الثعالب وتكررت القصة ومع مرور الوقت فأن معدل الارانب السريعة يزيد ويقل معدل الارانب البطيئة و مع مرور زمن اكبر فلمفلم يتبقى الا مجموعة من الارانب الاصلح للمعيشة(الاسرع)
وانتهت القصة بموت الضعفاء !!!!

بمعنى اصح ان البقاء للاقوى دائما ( الاقوى هنا تحسب حسب مقياس المشكلة التى سوف تعمل على حلها)

~تعالوا نطبق قصة العيش فى الغابة لعمل خوارزمية بسيطة!!!!

اذا كان لدى مشكلة ما ولها عدد لا حصر لة من الحلول واريد ان اجد او ابحث عن افضل حل لها ماذا افعل؟؟

باستخدام نظرية الافتراض؟
نفترض ان
مجموعة الحلول solution هو مجموعة الارانب
جودة الحل(دالة الهدف) fitness function هى مقياس سرعة الارانب او بطئها
عملية التزاوج هى عملية سوف ننشأها لتبادل اجزاء الحلول وسوف نطلق عليها crossover
فرصة المعيشة للارنب نتيجة الحظ سوف نجعلها بطرق متعددة للاختيار للحلول من جيل لاخر ونسميها selection
نضيف جزء الطفرة؟؟حيث انة يمكن ان يحدث بتغيير فى جين ما لحل ان ينتج عنة حل افضل وتسمى mutation

~اية رأيكم نكتب ما افترضنا على صورة خطوات :
اذا بداية لدى مجموعة من الارانب initial population( الحلول لمشكلة ما ) نطلق عليها (P(t اى P هى المجموعة الاولى( الجيل الاول) فى اللحظة الزمنية t سوف نقوم بعمل فرز لهم وذلك عن طريق مقياس لخصائص فيهم ونسمية fitness function هذة الخطوة تسمى (evaluate(t
ثم نبدا من هذا الجيل بحلقة تكراية تنتهى او تتوقف حتى تحقق بشرط ما (نضعة نحن طبقا للمشكلة النى نعمل على حلها)
ما الذى سوف يحدث فى هذة الحلقة
1-سوف نختار الافضل منهم (select P(t ليخضعوا لخطوتين التاليتين
2- عملية التزاوج بين افراد المجموعة لينتج جيل جديد crossover
3- يحدث بعض الطفرات وتسمى mutation وتحدث على مستوى الفرد (الارنب-الحل الواحد)
ثم نرجع ونعمل للجيل الجديد الحالى تقيم (evaluate P(t ويخضع للخطوات السابقة حتى ينتهى الشرط للحلقة التكرارية
4-نجد ان ما سوف نحصل علية افضل ارنب ( او بمعنى اصح افضل حل للمشكلة)

~نعيد كتابتها بطريقة رياضية اكثر وبأسلوب افضل

 

CODE: تحديد الكل

   1.[Start] Generate random population of n chromosomes (suitable solutions for the problem)
2. [Fitness] Evaluate the fitness f(x) of each chromosome x in the population
3. [New population] Create a new population by repeating following steps until the new population is complete
1.[Selection] Select two parent chromosomes from a population according to their fitness .
2.[Crossover] With a crossover probability cross over the parents to form a new offspring (children).
3.[Mutation] With a mutation probability mutate new offspring at each locus (position in chromosome).
4.[Accepting] Place new offspring in a new population
4.[Replace] Use new generated population for a further run of algorithm
5.[Test] If the end condition is satisfied, stop, and return the best solution in current population
6.[Loop] Go to step 2


~الان   لفهم  خوارزمية الجينات الوراثية
لدينا اربع نقاط مهمة اذا اردنا تطبيق خوارزمية الجينات الوراثية
problem representation :: encoding :عملية التمثيل لحل المشكلة ؟كيف سيتم تمثيل الحل لمشكلة ما
How to select best solution:: selection :: كيف يتم اختيار مجموعة من الحلول ليتم عليها عمليات الcrossover ,mutation
crossover::كيف يتم تبادل اجزاء من الحلول ليتم الحصول على حلول جديدة ترث من الحليين الابويين
mutation::كيف يمكن تغيير فى جزء من حل ليتم الحصول على حل جديد طفرة ربما يكون افضل وربما يكون اسوء

 

 

 

“The traveling salesman problem, or TSP for short, is this: given a finite number of ‘cities’ along with the cost of travel between each pair of them, find the cheapest way of visiting all the cities and returning to your starting point.”

ما هى مشكلة البائع المتجول:

لنفترض في دولة ما .. هنالك بائع لاغراض ما .. يتجول بين مدن هذه الدولة .. والمدن مبعثرة أي لا تقع على خط مستقيم لكنه يعرف الطرق التي تربط بين هذه المدن كلها .. فكر هذا البائع بان يمر بكل هذه المدن .. لكن بشروط :-

1. لا يمكن ان يكون البائع فى مدينتيين فى وقت واحد”زمن واحد”
2. المدينة يمر منها مرة واحدة فقط ولا يعود اليها ثانية .
3. اخيرا هو يجب علية ان يجد اقصر الطرق التي تجعله يمر بكل المدن ويعود الى مدينتة

 

 

هذا فلاش توضيحى اكثر
http://www.alaws2006.com/vb/showthread.php?t=46236

http://en.wikipedia.org/wiki/Travelling … an_problem

ما هى الصعوبة فى مشكلة البائع المتجول وما هى اهميتها وتطبيقتها فى الحياة؟؟؟

~اولا ::الصعوبة :

نتخيل لو لدنيا اربع مدن يجب على البائع زيارتهم هم A,B,C,D
فان عدد احتمالات الطرق التى ممكن ان يسلكها تحسب بالقانون

CODE: تحديد الكل

number of paths=n(n-1)/2 

حيث n هو عدد المدن

لو افترضنا لدينا 4 مدن فأن عدد المسارات التى يمكن ان يسلكها هى 6
لو افترضنا لدينا 100 مدينة فأن عدد المسارات التى يمكن ان يسلكها هى 4950
لو افترضنا لدينا 1000 مدينة فأن عدد المسارات التى يمكن ان يسلكها هى 499500
اذن نجد كلما زاد عدد المدن كلما زاد عدد المسارات الممكنة (الحلول الممكنة للمشكلة والذى اريد ايجاد افضل حل من بينهم) اى انة لدى عدد هائل من الحلول واريد ايجاد الافضل من بينهم –اذا كملخص صعوبة المشكلة انة كلما زاد حجم المشكلة كلما زاد الفضاء للبحث عن افضل حل لها

~ثانيا::اهمية المشكلة وتطبيقتها :

طبعا مشاكل كثيرة يمكن ان تكون جزء من مشكلة البائع المتجول مثلا
~فى الانتقالات (transportation) ترتيب المسارات للباصات التى توصل الطلبة الى المدارس او توزيع المنتجات الزراعية بين مجموعة من المدن
~فى صناعة الدوائر المنطقية وترتيبها
~فى routing ايصال الباكت data عبر اجهزة شبكة ما (حالة خاصة حيث لا يلزم المرور على كل الاجهزة)

بعدما تعرفنا على مشكلة البائع المتجول الان نريد ان نطبق الخوارزميات الجينية عليها لحلها

 

سوف نطبق خطوة خطوة STEP BY STEP~ كطفل صغير يحبو!

~الخطوة الاولى::تمثيل المشكلة problem representation :: encoding :عملية التمثيل لحل المشكلة ؟كيف سيتم تمثيل الحل لمشكلتنا

بداية تمثيل اى مشكلة هو الاصعب فى الخوارزميات الجينية لانة يعتمد بشكل كبير على فهم المشكلة واختلاف التمثيل يؤثر تماما فى الخطوات الاخرى للخوارزمية كما يؤثر فى النتيجة والوقت
عندما نقول تمثيل اى مشكلة:فيجب عليكم اعطائى شيئين ::
اولا :طريقة صياغة الحل الواحد للمشكلة
ثانيا :دالة الهدف التى تعتمد على شكل هذا الحل

اولا:طريقة صياغة المشكلة هناك عدة طرق لصياغة اى مشكلة او عمل تمثيل لها وهذا يجعلنا نتطرق الى kind of encoding

~انواع التمثيل kind of encoding:

Binary Encoding :

ويتم فية تمثيل الحل باستخدام 0 و 1 حيث الحل عبارة عن مجموعة من الاصفار والوحايد التى تعبر عن حل للمشكلة

~نطبق على مشكلتنا البائع المتجول:لو اننا استخدمنا مصفوفة ثنائية الابعاد وافترضنا ان كل صف يمثل مدينة وكل عمود يمثل ترتيبها فى الزيارة (الرحلة ) للبائع المتجول فاننا حصلنا على تمثيل ثنائى للمشكلة -ننظر للصورة

للتوضيح اكثر نفترض كما فى الصورة لدينا سبع مدن نرمز لهم {A,B,C,D,E,F,G} لو كما بالصورة قمنا بانشاء مصفوفة ثنائية الابعاد كل بعد طولة يبلغ عدد المدن لدى فى المشكلة 7 فاننا نستطيع ان نقول
المدينة A تم زيارتها السابعة المدينة C تم زيارتها الاولى المدينة D تم زيارتها الثالثة وهكذا فان الحل النهائى يكون

CODE: تحديد الكل

Solution s={C-F-D-G-E-B-A}

هذا هو التمثيل طيب ماذا عن دالة الهدف التى قلت عليها حتى يكون تمثيل صحيح -دالة الهدف سوف تكون عبارة عن شروط للتأكد من ان الحل صحيح

حيث الجزء الاول شرط ان عدد الوحايد فى الصفوف تكون n هو عدد المدن -الجزء الثانى شرط ان عدد الوحايد فى الاعمدة مساوى n عدد المدن -الجزء الثالث هو شرط ان عدد الوحايد فى الصفوف والاعمدة(فى المصفوفة ككل )مساوى n الجزء الاخير هو لحساب المسافة بين المدن

نلاحظ ان دالة الهدف ما هى الا تطبيق لشروط نجاح رحلة البائع المتجول
فيجب ان يكون كل عمود بة واحد فقط لانة لا يمكن ان يزور مدينيتن وقت واحد
ويجب ان يكن كل صف بة واحد فقط لانة لا يمكن ان يزور المدينة اكثر من مرة
ويجب ان يكون عدد المدن التى يزورها فى النهاية هى n من المدن
اخيرا يجب ان تكون رحلة امنة وليس فيها مشقة فنحسب اقل مسافة بين المدن

لكن هذا التمثيل لة عيب كبير انة كلما زاد حجم المشكلة كلما زاد حجم الذاكرة المستخدمة غير ان طرق الcrossover ,mutation تكون سهلة فى تطبيقها على هذا النوع من التمثيل لكن تؤدى دائمة الى كارثة وهى ان الحل الناتج يكون غير صحيح ويحتاج الى دوال للتصحيح validation “~سوف نتطرق لهذا مرة اخرى فيما بعد~”

Permutation Encoding ::
وفية يتم التمثيل “بارقام صحيحة او حروف “وهو سهل جدا والاغلب استخداما لدى المبرمجيين

~نطبق على مشكلتنا البائع المتجول:
لو لدينا 7 مدن يمكن ان يكون الحل هو

CODE: تحديد الكل

Solution s={ 1 4 7 3 5 6 2}

 

طبعا سهل لا يحتاج لشرح

طيب دالة الهدف ايضا بسيطة باعتبار ان π هى الرحلة فان الجزء الاول يحسب المسافة بين المدينة i التى تليها فى الرحلة -اما الجزء الثانى فلحساب المسافة للعودة الى المدينة رقم البداية

طبعا هناك انواع اخرى للتمثيل ويمكن ان يصمم اى منا تمثيل خاص لة بالمشكلة حسب وجهة نظرة لكن ايضا يجب ان يوجد دالة هدف لهذا التمثيل الجديد لحساب قيمة الحل النهائى

انواع اخرى للتمثيل encoding هنا
http://www.obitko.com/tutorials/genetic … coding.php

 

~الخطوة الثانية :
How to select best solution:: selection :: كيف يتم اختيار مجموعة من الحلول ليتم عليها عمليات الcrossover ,mutation

~طرق الselection

:Roulette Wheel Selection~
وفية يتم اختيار الحلول اعتمادا على جودة هذا الحل (قيمة دالة الهدف تكون كبيرة لو المشكلة maximization-وتكون صغيرة لو minimization

لو تخيلنا كما بالشكل اننا مثلنا جودة كل حل بمقدار ما اخذة من مساحة الدائرة فالحل الاول باللون الازرق اخذ مساحة كبيرة وهذا يعنى انة سوف يتم اختيارة لانة جودتة كبيرة (قيمة دالة الهدف للمشكلة جيدة) اما الحل باللون الاصفر فنسبة اختيارة اقل لان جودة الحل ليست كبيرة

اذا فى roulette wheel يتم اختيار الحلول حسب جودتها فالحل ذو قيمة افضل نسبة اختيارة ليكون فى الجيل الذى ستتم علية عملية crossover ,mutation كبيرة
هذا pseudo code لها

[Sum] Calculate sum of all chromosome fitnesses in population-sum S.
[Select] Generate random number from interval (0,S) - r.
[Loop] Go through the population and sum fitnesses from 0 - sum s.
When the sum s is greater then r, stop and return the chromosome where you are.

الكود طبعا بيختلف حسب المشكلة -لكن هذا كود كتبتة

 public final static  LinkedList<Solution>  roulewheelSelection(
LinkedList<Solution> pop,
int numToSelection)
{
LinkedList<Solution> selected = new LinkedList<Solution>();
double curr=0;
double sum = 0;
//  step 1- sum all fitness in population//
for(Solution s: pop)
sum=sum+s.fit;

while( selected.size()<numToSelection){ //select  number of solution equal numToSelection//  step 2- generate random number
double q=Math.random();   //q = [0,1)
//step 3 loop through solution to find the one with firness greater than q
for(Solution s: pop) {
curr= curr+s.fit/sum;
if(curr>=q){
selected.add(s);
break;
}
}
}
return selected;
}

 

Tourment Selection~
وهى طريقة لاختيار مجموعة من الحلول من population (الجيل الحالى) حيث نحدد بدايةَ عدد الحلول التى نريد اختيارها من population ثم نحدد عدد tournament size ونكرر لعدد الtournament size اختيار عدة حلول عشوائية من population ومنهم نختار الافضل فى كل مرة -نلاحظ ان يمكن ان يتم اختيار حل اكثر من مرة (تكرار اختيارة) لذا يمكن عندما يتم اختيار حل يتم الغاؤة من population

http://en.wikipedia.org/wiki/Tournament_selection

 

elitistSelectionStrategy~
وهى طريقة لاختيار جزء الحلول الافضل من الpopulation والغاء باقى الحلول منة هذة الاسهل على الاطلاق

هناك ايضا طرق كثيرة للselection ويمكن ان تعمل طريقة خاصة بكم وليس لها شروط هذة المرة

 

~الخطوة الثالثة : وهى خطوة انشاء جيل جديد وتتم بواسطة خطوتين crossover -mutation نبدأ بخطوة خطوة

-crossover::كيف يتم تبادل اجزاء من الحلول ليتم الحصول على حلول جديدة ترث من الحليين الابويين

اذن من التعريف عملية الcrossover هى عملية سوف تكون مسئولة عن تبادل بعض اجزاء من الحلول (بين ابويين -حليين) لينتج حلول جديدة ترث من هذين الحليين الاوليين (عملية الcrossover يجب ان تتم بين حليين على عكس عملية الmutation )

يوجد لدينا اكثر من طريقة لcrossover

Single point crossover~

فيها يتم اختيار نقطة عشوائية ويتم قطع الحليين عندها ويتبادل الاجزاء بينهما -ننظر للصورة لو لدينا حليين ابويين parent 1, parent 2 وافترضنا اختيار النقطة رقم 5 فيكون الناتج كما بالصورة child 1, child2

~Two point crossover

فيها يتم اختيار نقطتين عشوائيتين ويتم قطع الحليين عندهما ويتبادل الاجزاء بينهما

هناك طرق اخرى للcrossover يمكن البحث فى google

طيب هذا الcrossover لو كان الحل ممثل بbinary encoding ماذا لو كان الحل ممثل بPermutation Encoding | هو نفس المبدأ لا يتغير

طيب اية رايكم نطبق شوية على البائع المتجول : سوف نطبق ونحن نمثل الحل باستخدام الPermutation Encoding

ننظر للصورة لو اردنا تطبيق الSingle point crossover على الحليين الابويين فى الصورة ماذا سوف يحدث؟؟

ما هذا الحلول الناتجة عن عملية الcrossover حلول غير صحيحة حيث تكرر زيارة المدينة 2 مرتيين فى الرحلة وهذا غير محقق لشروط المشكلة؟؟
اذن ماذا نفعل ؟؟

اذن ما الحل الان ابدا   بوضع طرق من فهمك للمشكلة – اقصد اذا كنت تحل مشكلة ما باستخدام الخوارزميات الجينية وطرق الcrossover ,mutation المعروفة والمعتادة لا يمكن تطبيقها فيمكن من فهمكم للمشكلة ان تصنعوا طرق جديدة وتحسب جودة فعليتها على برنامجكم

طيب كيف اصنع طريقة crossover تضمن لى عدم تكرار المدن وان الحلول الناتجة تكون صحيحة –نعطى لمحة بسيطة من ضمن الطرق التى ىسوف نستخدمها عند التطبيق
~Partially-Mapped Crossover
حقيقة اجد الكثير يسأل عن شرحها وطريقة عملها ونقدمة لكم بأذن الله
Partially-Mapped Crossover
ومن اسمها فيها يتم عمل mapping جزئى اى لاجزاء من الحل
نفترض ان لدينا حليين :

Parent1: 2 5 0 3 61 4 7 
Parent2: 3 4 0 7 25 1 6

لو افترضنا اننا اخذنا مجموعة من المدن وقمنا بعمل mapping لهم ماذا سوف يحدث؟
~ فى parent1 نفترض اننا سوف نقوم بعمل map للمدينة رقم 3 ونضع ما يقابها مدينة رقم 7 فى الparent 2
~ فى parent1 نفترض اننا سوف نقوم بعمل map للمدينة رقم 6 ونضع ما يقابها مدينة رقم 2 فى الparent 2
~ فى parent1 نفترض اننا سوف نقوم بعمل map للمدينة رقم 1 ونضع ما يقابها مدينة رقم 5 فى الparent 2
غير واضح ممكن توضح اكثر -نعم انظروا للرسمة فما اريدة هو عمل mapping بين المدن فى الحليين الابويين

لعمل mapping :اتبع الخطوات الاتية

الخطوة الاولى :قم بعمل تبديل بين المدن 3و7 فى الابويين بمعنى كلما تجد المدينة 3ضع مكانها 7 والعكس الناتج

Child1: 2 5 0 7 6 1 4 3 
Child2: 7 4 0 3 2 5 1 6

الخطوة الثانية :قم بعمل تبديل بين المدن 2و6 فى الابويين بمعنى كلما تجد المدينة 2 ضع مكانها 6 والعكس الناتج

Child1: 6 5 0 7 2 1 4 3 
Child2: 7 4 0 3 6 5 1 2

الخطوة الاخيرة :قم بعمل تبديل بين المدن 5و1 فى الابويين بمعنى كلما تجد المدينة 1ضع مكانها 5 والعكس الناتج

Child1: 6 1 0 7 2 5 4 3 
Child2: 7 4 0 3 6 1 5 2

هذا ينتج لنا الحلول الابناء الاتية :

Parent1: 2 5 0 3 6 1 4 7 
Parent2: 3 4 0 7 2 5 1 6
Child1: 6 1 0 7 2 5 4 3
Child2: 7 4 0 3 6 1 5 2

 

mutation~:: وتعرف بالطفرة من علم الوراثة وفيها يتم تغيير جين ما بطريقة عشوائية لينتج صفة ليست فى الاب او الام -بالنسبة لنا نقصد بها كيف يمكن تغيير فى جزء من حل ليتم الحصول على حل جديد ” ربما يكون افضل وربما يكون اسوء من الحل قبل الطفرة”

طرق الmutation كثيرة وسوف نعرض منها مجموعة كثيرة حقيقة اجد لها تأثير افضل من crossover فى معظم البرامج التى اعمل عليها

~Exchange Mutation: وفية يتم تبادل بين two genes تم اختيارهم بشكل عشوائى

نطبق على البائع المتجول :لو لدينا حل متمثل بالرحلة الاتية

path =5 3 2 1 7 4 0 6

فيمكن الحصول على حل جديد باختيار مدينتين بشكل عشوائى ويتم تبديل المواقع لهم فى الرحلة-فمثلا اذا قلما اننا تم اختيار المدينيتن 7 و5 فأننا نحصل على حل جديد ويتمثل ب
path =7 3 2 1 5 4 0 6

Displacement Mutation~:
وفية يتم اختيار two genes بشكل عشوائى ويتم اخذ مجموعة الgenes التى بينهم كمجموعة ويعاد وضعهم فى الحل من اى نقطة عشوائية

مثال :على البائع المتجول ايضا لو افترضنا لدينا الحل الاتى

p1=0 1 2 3 4 5 6 7
وتم اختيار الموقعين رقم 4 و6 فان مجموعة الجين 345 سوف يتم اعادة وضعهم فى الحل فى اى نقطة عشوائية من البداية سوف نحصل على

c1=0 3 4 5 1 2 6 7

Insertion Mutation~:
وفية يتم اختيار gene عشوائى ويتم ازالتة من الحل ويعاد وضعة فى موضع عشوائى فى الحل

نطبق على البائع المتجول : لو لدينا الحل الاتى:

p1=0 1 2 3 4 5 6 7
وافترضنا اننا تم اختيار المدينة رقم 2 فاننا لنطبق الinsertion سوف نزيل المدينة 2 من الحل ليصبح

p1=0 1 3 4 5 6 7

ثم نحدد نقطة عشوائية لاعادة وضعها ليصبح الحل كالاتى
c1=0 1 3 4 5 2 6 7

هناك العديد والعد من الطرق لعمل طفرة ليتكون حل جديد

الى هنا انتهينا من شرح جميع الخطوات -الحمد الله رب العالميين

التطبيق العملى هناك اكواد كثيرة جدا فى google متاحة عن المشكلة وحلها بالخوارزميات الجينية سوف اعرض مقاطع من الاكواد

 

 

اولا: قبل البدء فى الخوارزمية نحدد مدخلات المشكلة ومخرجاتها (المدخلات مجموعة من المدن- المخرجات اقصر رحلة يمكن ان يسلكها السائق)

اذن الخطوة الاولى : قراءة ملف المدن التى سوف يزورها السائق(لكن من اين احصل على مجموعة مدن ومسافات بينها احد الحلول توليد مجموعة عشوائية من المدن -حل اخر هناك موقع يعرض قاعدة بيانات عن مجموعة من المدن )

http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/
فلنعمل من هذا الموقع لماذا ؟ لان اى احد يقوم بعمل بحث للنشر فى هذة المشكلة يستخدم standard data ويقارن نتائجة مع الاخريين لذا احببت ان اقرأ الملفات منة لنستخدم نفس data-سوف نحمل ملف ونعمل على قرائتة

~نكتب كود لميثود لقراءة الملف

public static void readData(){
BufferedReader file;
try {
file = new BufferedReader(new FileReader("cities.txt"));
String text=null;
int  i=0;
try {
while((text=file.readLine())!=null){
String [] line=text.split(" ");
x[i]=Double.parseDouble(line[1]);
y[i]=Double.parseDouble(line[2]);
i++;  

}

} catch (NumberFormatException ex) {
ex.printStackTrace();
} catch (IOException ex) {
ex.printStackTrace();
}
} catch (FileNotFoundException ex) {
ex.printStackTrace();
}
}

 

بعد ما قمنا بقراءة ملف المدن نبدأ بخطوات الخوارزمية

~ تمثيل حلencoding: سوف نستخدم permutation encoding اى ان الحل عبارة عن مجموعة من الارقام التى تعبر عن رقم المدينة
الان نريد ان ننشىء حل عبارة عن مجموعة من الارقام ليست متكررة لان السائق لا يمكن ان يزور المدينة الواحدة اكثر من مرة
هذة ميثود لتوليد ارقام عشوائية ليست متكررة

public static int[] createPermutation(int start,int end){
int minValue = start;
int maxValue = end;
int numInts =end;  

int range = maxValue - minValue;
int[] randomInts = new int[numInts];
int nextRandom;
for (int i = 0; i < numInts; i++) {
nextRandom = r.nextInt(range + 1) + minValue;
randomInts[i] = nextRandom;
// now check the digits we already have
for (int j = 0; j < i; j++) {
if (nextRandom == randomInts[j]) {
i--; // duplicate, try again
j = i; // short-circuit inner-loop
}
}
}
return randomInts;
}

 يمكنكم تكملة  اجزاء الكود بأذن الله تعالى

ملحوظات

من المشاكل التى تقابلنا فى الخوارزمية الجينية هى ان بعد مرور فترة من التكرار للعمليات selection- crossover-mutation نجد الpopulation بقى حل واحد (وقع فى local minimum ) لا تؤثر فية الcrossover ولا muation

ترى كيف احل هذة المشكلة : بعض الاقتراحات:

1-الحل الاول :امنع الحلول المتشابهة فى population لكن عيبها
-اولا :وقت اطول للحصول على حلول جديدة
-ثانيا-هل فى المشكلة التى نحن نحلها طريقة سهلة لنعلم بها كيف نحصل على دالة للتشابهة بين الحلول

2- الحل الثانى:اغير فى طرق الcrossover ,mutation -ممكن لكن سوف نعود لنفس النقطة ان بعد فترة من تكرارها نحصل على حلول متشابهة

3-الحل الثالث :احاول وضع مجموعة من الحلول عشوائية فى الpopulation

4-الحل الرابع:احاول عدم رفض كل الحلول الغير جيدة ربما عند تطبيق crossover ,mutation مع حلول جيدة ينتج حلول افضل من الاثنيين (وكأننا نهرب مثل الsimulation anneling من  local optimall

 ——————————————

مراجع:
http://gaul.sourceforge.net/
http://www.c-sharpcorner.com/UploadFile … rithm.aspx
http://www.codeguru.com/cpp/misc/misc/a … php/c3795/
http://www.obitko.com/tutorials/genetic … coding.php
http://mnemstudio.org/genetic-algorithms-mutation.htm
http://www.scribd.com/doc/53306810/30/UNIFORM-CROSSOVER
http://en.wikipedia.org/wiki/Crossover_ … gorithm%29

 

الحمد الله رب العالميين حمدا كثيرا مباركا فية