تعد الـ Hash Table من أهم وأسرع هياكل البيانات على الإطلاق، وكثير من التطبيقات تستخدم مثل هذه البنيه مثل Spell Checker أو Symbol Table في المترجمات، حيث تضمن لنا هذه البنيه الوصول السريع جدا لأي بيانات نريدها مهما كان حجم تلك البيانات، بالاضافه الى ادخال البيانات أيضا يتم في سرعه كبيره .. زمن التنفيذ لها هي ((O(1) وبالتالى تعد من أسرع هياكل البيانات على الإطلاق (مثلها مثل المصفوفه) ،، اضافه الى ميزه السرعه هناك ميزه جيده بها وهي أنها سهله التطبيق حيث أننا سنطبق هذه البنيه من خلال مصفوفه عاديه أو vector.
بالرغم من ميزات هذه البنيه ، الا أنها يجب أن تستخدم في الأوقات المناسبه وقد لا تصلح لكل حاله ،، لأن الHash Table أولا يتم تطبيقه باستخدام المصفوفه Array والتي يصعب توسيعها (لكننا سنتجاوز هذه المشكله لأننا سنستخدم vector) ، ثانيا وهو الأهم أن أداء هذه البنيه يقل تدريجيا كلما أمتلئت المصفوفه table ، لذلك من البدايه يجب أن نحدد حجم البيانات التي سوف توضع في هذه المصفوفه ونقوم بحجز مساحه مناسبه لهذا الحجم ..ثالثا باستخدام الHash Table لا يمكن زياره جميع العناصر في المصفوفه (بمعنى أصح لا توجد فائده من هذه العمليه Visiting لأن البيانات مخزنه في أماكن عشوائيه بلا ترتيب) ، وبالتالى لا يمكنك مثلا اجراء عمليه ايجاد القيمه الأكبر في هذه البنيه Find Max ، وفي حال أردت أن تستخدم بنيه توفر لك هذه الميزه فإن الBinary Tree بكل تأكيد هي الأنسب في هذه الحاله .
الHash Table يفضل أن تستخدم في حال كانت البيانات التي تتعامل معها ثابته ولا تتغير ، وتريد الوصول لها في كل مره بشكل سريع ، مثلا البرامج التي تستخدم القاموس Dictionary يمكن أن تقرأ هذه القاموس وتضعه في بنيه Hash Table في الذاكره وقت تشغيل البرنامج.
برمجة ال Hash Table
أحد أهم المفاهيم في الHash Table والHashing بشكل عام هو كيف يمكن تحويل مجموعه من المفاتيح الى مواقع معينه Index في المصفوفه ، في أبسط الأحوال لا تكون هناك أي عمليه تحويل ويكون المفتاح هو نفسه مباشره الموقع Index في المصفوفه ، لكن هناك حالات أخرى كثيره لا يكون هناك مفتاح من أساسه وبالتالى عمليه التحويل من أي قيمه الى موقع index سوف تتم باستخدام الداله المعروفه بالHash Function .
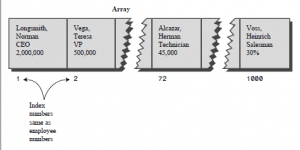
نبدأ بأبسط حاله ممكنه وهي استخدام المفتاح كموقع index ، ولنفرض أنك تريد برمجه نظام لشركه صغيره تحتوي على 1000 عميل وكل سجل عميل يتطلب حوالى 1000 بايت ، بالتالى المجموع الكلي للبيانات هي 1 Megabyte وبكل تأكيد يمكن تحميل هذه القاعده الى الذاكره مباشره وقت تشغيل البرنامج ،،
أسهل حل ممكن وأسرع حل أيضا هو عمل مصفوفه من السجلات تتكون من 1000 خانه ،، وفي حال أردنا أن نستعلم عن العميل محمد صاحب الرقم 300 فكل ما في الأمر :
Record mohmmed = dataBaseArray[300];
أيضا في حال جاء عميل جديد للشركه فيمكن أن نضيف بياناته على النحو :
Record ahmed = new Record; dataBaseArray[count++] = ahmed;
في مثل هذه الحاله أو أي حاله مشابه لها وهو وجود مفتاح معين لكل سجل فيمكن أن نستخدم هذا المفتاح كموقع في المصفوفه Keys Are Index Numbers وبالتالى الوصول لأي موقع سيكون أسرع ما يكون على الإطلاق Big-o (1) .
لكن بالطبع في الكثير من الأحيان لن تجد لديك أي مفتاح وستجد قيم مختلفه (نص string مثلا) وهنا سوف تكون مهتمك هو إيجاد أي وسيله لكي تحول هذا النص الى موقع Index .نأخذ مثال صغير على قاموس يحتوي على 50000 كلمه ، ونريد أيجاد أسرع طريقه يمكن من خلالها ايجاد كلمه معينه . في البدايه سنقوم بعمل مصفوفه من 50000 خانه ،، الأن مثلا نريد أن نبحث أو ندخل الكلمه person ، السؤال هنا كيف يمكن أن نجد الموقع المناسب index لهذه الكلمه؟
الحل الأول والأسهل اطلاقا هو تحويل كل حرف الى رقم ومن ثم جمع هذه الأرقام (Add the Digits) ، ومن ثم تمثل لي مجموع هذه الأرقام الموقع في المصفوفه index (سوف نعطي الحرف a القيمه 1 وb القيمه 2 وهكذا ..اضافه الى حرف المسافه space سوف نعطيه مثلا القيمه 0 ، وبالتالى مجموعه الحروف هنا 27).
مثلا الكلمه cats سوف نقوم بتحويلها بهذ الطريقه وينتج لدينا :
3 + 1 + 20 + 19 = 43
وهكذا الكلمه cats سوف تكون موجوده أو سوف نقوم بتخزينها في الموقع 43 .. وهكذا لبقيه الكلمات ،، نأخذ كلمه أخرى ولنفرض أن القاموس الذي نحن بصدده تتكون فيه الكلمات من حرف الى 10 حروف على الأكثر ، بالتالي تكون الكلمه الأولى في القاموس a مخزنه في الموقع 1 :
0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
والكلمه الأخيره zzzzzzzzzz مخزنه في الموقع :
26 + 26 + 26 + 26 + 26 + 26 + 26 + 26 + 26 + 26 = 260
بدأت المشاكل بالظهور !!
لدينا قاموس يتكون من 50000 كلمه ،، والكلمه الأولى تخزن في الموقع الأول ، والأخيره تخزن في الموقع 260 .. اذاً جميع الكلمات سوف تخزن في الخانات ما بين 0 الى 260 (أي أن لكل خانه في المصفوفه هناك 192 كلمه يجب أن تخزن وذلك بقسمه 260 على 50000) . هنا يمكن تطبيق هذه العمليه بجعل المصفوفه تكون مصفوفه من المؤشرات ، وكل من هذه المؤشرات يرتبط بمؤشر وهكذا ، أي مصفوفه من الLinked list وكل واحده من هذه الlist سوف نخزن فيها ال192 كلمه ..
بالرغم من أننا حللنا المشكله ، ولكن عمليه البحث في Linked List مكلفه أيضا وخصوصا في حال كبرت البيانات O (m) .لذلك في الحل الأول Add the Digits بالرغم من صغر حجم المصفوفه الى أننا نريد أن نسرع عمليه البحث بأكبر شكل ممكن ..
الحل الأخر وهو بأن نضرب كل حرف ب26 مرفوع له القوى i حيث هي موقع الحرف ، مثال للكلمه cats :
3*27^3 + 1*27^2 + 20*27^1 + 19*27^0 = 60,337
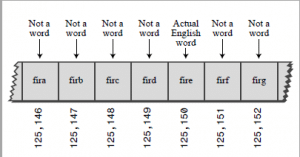
على ما يبدوا أن هذا الحل سوف يولد لكل كلمه ممكنه موقع فريد ، ننظر الى الكلمه zzzzzzzzzz وفقط نحسب الz الأخيره وهي 26*27^9 وهذا الرقم فقط أكثر من 7,000,000,000,000 !! للأسف مشكله هذه الطريقه أنها تولد خانات لأي كلمه ممكنه مثلا aaaaa,aaaaaa,aaaaaa وهكذا سينتج الكثير من الكلمات غير صحيحه من الأساس .
الحل الأول ولَد القليل من المواقع أقل من ما نحتاجه ، والحل الثاني ولد أكثر من ما نحتاجه بكثيير ،، ما العمل ؟
Hashing
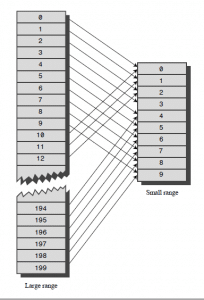
نحن بحاجه الى طريقه نستطيع من خلالها تحويل هذا الرقم الضخم الى رقم صغير مناسب يكون كindex في المصفوفه ،، السؤال هنا كم خانه نحن بحاجه اليها من الأساس ؟ بما أن القاموس يتكون من 50000 كلمه فنحن بحاجه الى عدد كافي من الخانات ،، لكن كما ذكرت من البدايه وسيتضح السبب فيما بعد يجب أن يكون الحجم الممتلئ من الhash table حوالى النصف أو 2/3 على الأكثر ، لذلك نقوم بحجز عدد كافي وليكن 100000 خانه ..
الأن نريد أن نحول الرقم الضخم الكبير 7,000,000,000,000 الى رقم صغير في حدود ال100000 ، وهذه هي الفكره الأساسيه من وراء الhashing ، وسوف نستخدم المعامل modulo باقي القسمه % لضمان وقوع أي رقم مهما كان في مجال معين ،،
arrayIndex = hugeNumber % arraySize;
نقوم بتطبيق بسيط داله تقوم بحساب الهاش للstring المرر لها :
int hashString (const string& str) {
int hashValue = 0;
int power = 1;
for (int i=str.length()-1; i>=0; --i) {
int letter = str[i] - 96; // get char code , assume char in small letter
hashValue += power*letter;
power *= 27; // next power
}
return hashValue % size;
}
داله الهاش يجب أن تكون سريعه لأننا سنجري هذه العمليه في كل مره نريد البحث أو الأدخال وبالتالى يجب أن نقلل من عمليات الضرب والقسمه ، ويمكن أن نستخدم عمليات الShifting بدلا من الضرب والقسمه لأنها الأسرع ، حاليا سوف نستخدم طريقه بسيطه لتحويل عمليه الضرب والرفع لأس الى عمليه ضرب وجمع ، تسمى طريقه هورنر نسبه الى عالم رياضيات ، وهي أن المعادله :
var4*n^4 + var3*n^3 + var2*n^2 + var1*n^1 + var0*n^0
يمكن أن تكتب :
(((var4*n + var3)*n + var2)*n + var1)*n + var0
الداله السابقه بعد تطبيق طريقه هورنر :
int hashString2 (const string& str) {
int hashValue = 0;
for (int i=0; i<str.length(); i++){
int letter = str[i] - 96;
hashValue = ( hashValue*27 + letter) % size;
}
return hashValue;
}
على العموم فأي داله hash كما تبين الصوره السابقه ستقوم بوضع أكثر من رقم في نفس الموقع وهذه المشكله تسمى التصادم Collisions وهذا هو الثمن الذي ستدفعه من جراء عمليه الhashing .ويستحيل بالطبع عمل perfect hashing وذلك بجعل كل كلمه في القاموس في موقع فريد ، لكن الذي نأمله هو عدم وجود كلمات كثيره في كل موقع .
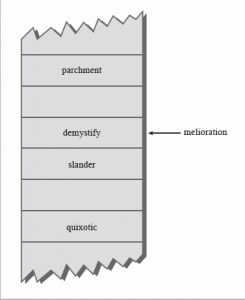
الصوره التاليه توضح عمليه التصادم ، حيث يحتوي الhash table على الكلمه demystify ، ونريد اضافه الكلمه الجديده melioration وبعد عمل hash لها تبين أن لها نفس الindex للكلمه demystify .
كيف سندخل هذه الكلمه الجديده للجدول ؟ بمعنى أصح كيف يمكن أن نحل التصادم هذا ؟ هناك طريقتين في الحل وسنتحدث عنهم في هذه المقاله ان شاء الله ،، الطريقه الأولى وتسمى open addressing تبدأ بالبحث من ذلك الموقع (المحجوز)عن أي خانه تاليه تكون فارغه وندخل فيها الكلمه الجديده ، لذلك ذكرنا قبل قليل أن حجم الhast table يجب أن يكون كبير أكبر من حجم البيانات الحقيقي ،،
الطريقه الثانيه وتسمى separate chaining وهي بجعل خانات المصفوفه تؤشر الى linked list of words أي كل خانه في المصفوفه لديه قائمه مرتطبه به ، وفي حال وجد تصادم في الموقع 10 نقوم بادخال هذه الكلمه في أخر القائمه في الموقع 10 .
الطريقه الأولى open addressing كما ذكرنا تعمل بالبحث من الموقع الحالى عن أي خانه فارغه لكي تضيف الكلمه الجديده ، وهناك 3 طرق أيضا لهذه العمليه وكل منها تحتلف في كيفيه ايجاد الخانه الفارغه التاليه ، فالطريقه الأولى Linear Probing تقوم بالبحث خانه خانه بدءا من الخانه التي حصل فيها التصادم ، أما الطريقه الثانيه quadratic probing تقوم بزياده خطوه البحث بشكل متصاعد يكون عباره عن مضاعفات كل خانه بالشكل :1 4 9 25 وهكذا ،، الطريقه الثالثه double hashing وهي الأفضل تقريبا ، حيث تقوم باعاده حساب الhash مره أخرى (بداله أخرى) لكي يتم ايجاد الموقع الجديد للكلمه ،، ستتضح الأمور مع الأمثله الأن .
Linear Probing
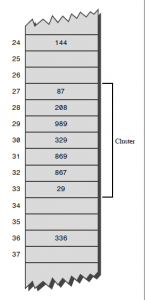
في حال حدث التصادم في الخانه i ، نقوم بالبحث من الخانه i+1 عن أي خانه فارغه لكي ندخل فيها هذه القيمه الجديده ،، هذه العمليه قد تسبب مشكله ما ، مثلا الكلمه الجديده حصل لها تصادم وأضفناها في الموقع i+1 ، وجائت كلمه جديده أخرى وحصل تصادم في نفس الموقع i سوف تضاف في الخانه i+2 .. لنفرض جائت كلمه جديده وكان لها hash جديد لكنه للأسف كان يساوي i+2 وبالتالى يحدث تصادم ، وهكذا سيكبر عدد التصادمات وتضاف القيم بشكل متسلسل ، هذه المشكله تعرف بClustering
وهكذا كل ما تمتلئ المصوفه كل ما زاد الClustering ، لذلك من البدايه ذكرنا يجب أن تكون حجمها كبير حتى نتلافي هذه المشاكل .
نقوم الأن بتطبيق Linear Probe Hash Table ، وحاليا للتبسيط المصفوفه سوف تكون من Data وهو كلاس يحتوي على int :
// Linear Probe Hash Table
#include <iostream>
#include <vector>
using namespace std;
class Data {
private:
int value;
public :
Data(int d):value(d) { }
void setData (int d) { value = d ; }
int getData () const { return value; }
};
class LinearHashTable {
private:
vector<Data*> hashTable;
int size;
public :
LinearHashTable (int size);
//
void insert (int key);
Data* remove (int key);
Data* find (int key);
//
friend ostream& operator << (ostream& ostr , const LinearHashTable& tbl);
private :
int hashFunction (int key);
};
LinearHashTable :: LinearHashTable (int size) {
hashTable.resize(size);
this->size = size;
//
for (int i=0; i<size; i++)
hashTable[i] = NULL;
}
void LinearHashTable :: insert (int key) {
Data* data = new Data(key);
int hash = hashFunction(key);
while (hashTable[hash] != NULL && hashTable[hash]->getData() != -1) {
hash++;
hash %= size;
}
hashTable[hash] = data;
}
Data* LinearHashTable :: remove (int key){
int hash = hashFunction(key);
while ( hashTable[hash] != NULL ){
if ( hashTable[hash]->getData() == key ) {
Data* tmp = hashTable[hash];
delete hashTable[hash];
hashTable[hash] = new Data(-1);
return tmp;
}
hash++;
hash %= size;
}
return NULL;
}
Data* LinearHashTable :: find (int key){
int hash = hashFunction(key);
while ( hashTable[hash] != NULL) {
if ( hashTable[hash]->getData() == key)
return hashTable[hash];
else {
hash++;
hash %= size;
}
}
return NULL;
}
int LinearHashTable :: hashFunction(int key) {
return key % size;
}
ostream& operator << (ostream& ostr , const LinearHashTable& tbl ) {
cout << "Content: ";
for (int i=0; i<tbl.size; i++){
if ( tbl.hashTable[i] != NULL )
cout << tbl.hashTable[i]->getData() << " ";
else
cout << "** ";
}
cout << endl;
return (ostr);
}
int menu () {
cout << "[1] insert value " << endl
<< "[2] find value " << endl
<< "[3] remove value " << endl
<< "[4] display table" << endl
<< "[5] exit " << endl
<< " >> ";
int choice;
cin >> choice;
return choice;
}
int main (int argc , char* argv[]) {
cout << "Enter Size of hash : ";
int size , key;
cin >> size;
//
LinearHashTable hashTable(size);
//
time_t aTime;
srand( static_cast<unsigned>(time(&aTime)));
for (int i=0; i<size/2; i++)
hashTable.insert( rand() % (10*size) );
//
bool state = true;
while ( state ) {
switch (menu()) {
case 1 :
cout << "Enter key to insert: ";
cin >> key;
hashTable.insert(key);
break;
case 2:
cout << "Enter key to find: ";
cin >> key;
if ( hashTable.find(key) != NULL )
cout << "Found key " << key << endl;
else
cout << "cannot found " << key << endl;
break;
case 3:
cout << "Enter key to remove : ";
cin >> key;
if ( hashTable.remove(key) != NULL )
cout << "remove key " << key << endl;
else
cout << "cannot found " << key << endl;
break;
case 4:
cout << hashTable << endl;
break;
case 5 :
state = false;
break;
}
}
return (0);
}
للأسف الطريقه الأولى Linear Probing تقوم بعمل كلستر وخاصه في حال أمتلئت المصفوفه (عمليه الإمتلاء تعرف بload factor ويتم حسابها عن طريق loadFactor = nItems / arraySize ) ومن هنا أتت الطرق الأخرى لحل هذه المشكله ،،
Quadratic Probing
وهذه الطريقه تعمل بنفس مبدأ الطريقه السابقه ولكن الزياده هنا لن تكون بمقدار واحد ، بل تكون بمضاعفه الموقع الحالى x بالشكل :
x+1, x+4, x+9, x+16, x+2
اي الزياده في المحاوله الأولى هي 1 ، ومن ثم في حال وجد ذلك المكان ممتلئ فتكون الزياده 4 وذلك لتجنب الكلستر في حال كان هناك كلستر موجود..وهكذا كل مره يتم القفر بخطوه كبيره ،،
بالرغم من أنها حلت مشكله الكلستر ، ولكنها أيضا صنعت مشكله كلستر أخرى secondary clustering وهي أن أي كلمه جديده لها نفس الهاش في الموقع i سوف تمر بجميع الخطوات 1و4و9 لكي تجد مكان فارغ ،، على العموم أداء الطريقه أفضل من الأولى ولكنها غير جيده أيضا لذلك لن نقوم بتطبيقها .. لنرى الطريقه الثالثه .
Double Hashing
مشكله الكلستر الأولى أن أي كلمه تصادمت سوف يتم القفز للخانه التاليه وهكذا ،، مشكله الكلستر الثانيه وهي أن كل تصادم يحدث سوف يتم القفز أيضا للخانه 1 ثم 4 ثم 9 وهكذا أي العمليه متسلسله وهكذا ينتج الكلستر ،، لحل هذه المشكلتين سنقوم بأخذ هاش أخر لنفس الكلمه بواسطه داله أخرى وبالتالى سينتج موقع جديد سوف يكون هو مقدار القفز step size لكل كلمه تصادمت وهذه العمليه تعرف باعاده الهاش Re-hashing ، هذه الداله الثانيه يجب أن لا ترجع قيمه 0 مهما كان (لأن القيمه ستكون قيمه قفز لموقع جديد) اضافه الى أنها بالطبع يجب أن تكون مختلفه عن الداله الهاشيه الأولى ،، وعاده يتم استخدام هذه الداله step:
stepSize = constant - (key % constant);
ويكون الconstant عدد أولى prime أقل من حجم المصفوفه ، اضافه الى أن حجم المصفوفه يجب أن يكون عدد أولى ، فمثلا في حال كان حجم المصفوفه 15 -غير أولى- وكان الثابت هو 5 ، فكل مره نستدعى داله الهاش الثانيه step سوف يكون الناتج أما 0 أو 5 أو 10 ولن تخرج بقيه العناصر الفارغه ، أما اذا العدد أولى مثلا 13 فسوف تخرج جميع العناصر .
نقوم الأن بتطبيق Double Hashing وسوف تلاحظ أن الأختلاف مع المثال السابق هو سطرين فقط في كل داله واضافه الداله الجديده :
// Double Hash Table
#include <iostream>
#include <vector>
using namespace std;
class Data {
private:
int value;
public :
Data(int d):value(d) { }
void setData (int d) { value = d ; }
int getData () const { return value; }
};
class DoubleHashTable {
private:
vector<Data*> hashTable;
int size;
public :
DoubleHashTable (int size);
//
void insert (int key);
Data* remove (int key);
Data* find (int key);
//
friend ostream& operator << (ostream& ostr , const DoubleHashTable& tbl);
private :
int hashFunction (int key);
int hashFunction2(int key);
};
DoubleHashTable :: DoubleHashTable (int size) {
hashTable.resize(size);
this->size = size;
//
for (int i=0; i<size; i++)
hashTable[i] = NULL;
}
void DoubleHashTable :: insert (int key) {
Data* data = new Data(key);
int hash = hashFunction(key);
int step = hashFunction2(key);
while (hashTable[hash] != NULL && hashTable[hash]->getData() != -1) {
hash += step;
hash %= size;
}
hashTable[hash] = data;
}
Data* DoubleHashTable :: remove (int key){
int hash = hashFunction(key);
int step = hashFunction2(key);
while ( hashTable[hash] != NULL ){
if ( hashTable[hash]->getData() == key ) {
Data* tmp = hashTable[hash];
delete hashTable[hash];
hashTable[hash] = new Data(-1);
return tmp;
}
hash += step;
hash %= size;
}
return NULL;
}
Data* DoubleHashTable :: find (int key){
int hash = hashFunction(key);
int step = hashFunction2(key);
while ( hashTable[hash] != NULL) {
if ( hashTable[hash]->getData() == key)
return hashTable[hash];
else {
hash += step;
hash %= size;
}
}
return NULL;
}
int DoubleHashTable :: hashFunction(int key) {
return key % size;
}
int DoubleHashTable :: hashFunction2(int key) {
return 5 - key%5;
}
ostream& operator << (ostream& ostr , const DoubleHashTable& tbl ) {
cout << "Content: ";
for (int i=0; i<tbl.size; i++){
if ( tbl.hashTable[i] != NULL )
cout << tbl.hashTable[i]->getData() << " ";
else
cout << "** ";
}
cout << endl;
return (ostr);
}
int menu () {
cout << "[1] insert value " << endl
<< "[2] find value " << endl
<< "[3] remove value " << endl
<< "[4] display table" << endl
<< "[5] exit " << endl
<< " >> ";
int choice;
cin >> choice;
return choice;
}
int main (int argc , char* argv[]) {
cout << "Enter Size of hash : ";
int size , key;
cin >> size;
//
DoubleHashTable hashTable(size);
//
time_t aTime;
srand( static_cast<unsigned>(time(&aTime)));
for (int i=0; i<size/2; i++)
hashTable.insert( rand() % (2*size) );
//
bool state = true;
while ( state ) {
switch (menu()) {
case 1 :
cout << "Enter key to insert: ";
cin >> key;
hashTable.insert(key);
break;
case 2:
cout << "Enter key to find: ";
cin >> key;
if ( hashTable.find(key) != NULL )
cout << "Found key " << key << endl;
else
cout << "cannot found " << key << endl;
break;
case 3:
cout << "Enter key to remove : ";
cin >> key;
if ( hashTable.remove(key) != NULL )
cout << "remove key " << key << endl;
else
cout << "cannot found " << key << endl;
break;
case 4:
cout << hashTable << endl;
break;
case 5 :
state = false;
break;
}
}
return (0);
}
الى الان تعرضنا الى طرق open addressing لحل مشكله الCollisions ، وسنعرض الأن الحل الأخر وربما الأفضل لحل مشكله التصادم وهو Separate chaining.
Separate chaining
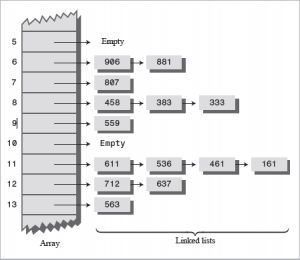
هنا سوف تكون لدينا مصفوفه ولكن كل خانه منها تؤشر الى قائمه مرتبطه linked list ، وبالتالى بعد عمل hash لأي كلمه ومعرفه الindex سنقوم بادخال هذه الكلمه في القائمه الموجوده في الindex ، وفي حال حدث التصادم سوف نضيف الكلمه أيضا في هذه القائمه ، وبالتالى سنكون أنهينا عمليه البحث عند حدوث التصادم ،
الLoad Factors هنا لا يهم اطلاقا ، وليس كما كان عندما كنا نستخدم أحد طرق الـopen addressing حيث يجب أن تكون عدد الخانات الممتلئه فيها على الأكثر2/3 ، أما في الSeparate chaining فلا مشكله وحتى اذا كانت المصفوفه ممتلئه كليا لأن أي خانه تحتوي على العديد من القيم (في القائمه) ،، لذلك نستخدم هذه الطريقه خصوصا في حال كنا لا نعلم عدد العناصر التي يجب وضعها في المصفوفه قبل البدء في البرنامج لأن الأمتلاء هنا لا يمثل مشكله ،،
تطبيق بسيط لل HashTable باستخدام Separate Chaining :
//separate chaining
#include <iostream>
#include <vector>
using namespace std;
class Data {
private:
int value;
Data* next;
public :
Data(int d):value(d),next(NULL) { }
//
void setData (int d) { value = d ; }
int getData () const { return value; }
//
void setNext (Data* d) { next = d; }
Data* getNext () const { return next; }
};
class SortedLinkedList {
private:
Data* first;
public :
SortedLinkedList();
//
void insert (int key);
void remove (int key);
Data* find (int key);
//
friend ostream& operator << (ostream& ostr , const SortedLinkedList& list);
};
SortedLinkedList :: SortedLinkedList (){
first = NULL;
}
void SortedLinkedList :: insert (int key){
Data* data = new Data(key);
//
Data* prev = NULL;
Data* current = first;
while ( current != NULL && key > current->getData()) {
prev = current;
current = current->getNext();
}
if ( prev == NULL )
first = data;
else
prev->setNext(data);
data->setNext(current);
}
void SortedLinkedList :: remove (int key) {
Data* data = new Data(key);
//
Data* prev = NULL;
Data* current = first;
while ( current != NULL && key != current->getData()) {
prev = current;
current = current->getNext();
}
if ( prev == NULL)
first = first->getNext();
else
prev->setNext(current->getNext());
}
Data* SortedLinkedList :: find (int key) {
Data* current = first;
while ( current != NULL && current->getData() <= key) {
if ( current->getData() == key )
return current;
current = current->getNext();
}
return NULL;
}
ostream& operator << (ostream& ostr , const SortedLinkedList& list) {
ostr << "Content: ";
Data* current = list.first;
while ( current != NULL ) {
ostr << current->getData() << " ";
current = current->getNext();
}
ostr << endl;
return ostr;
}
class HashTable {
private:
vector<SortedLinkedList*> hashTable;
int size;
public :
HashTable (int size);
//
void insert (int key);
void remove (int key);
Data* find (int key);
//
friend ostream& operator << (ostream& ostr , const HashTable& tbl);
private :
int hashFunction (int key);
};
HashTable :: HashTable (int size) {
hashTable.resize(size);
this->size = size;
//
for (int i=0; i<size; i++)
hashTable[i] = new SortedLinkedList;
}
void HashTable :: insert (int key) {
int hash = hashFunction(key);
hashTable[hash]->insert(key);
}
void HashTable :: remove (int key){
int hash = hashFunction(key);
hashTable[hash]->remove(key);
}
Data* HashTable :: find (int key){
int hash = hashFunction(key);
return hashTable[hash]->find(key);
}
int HashTable :: hashFunction(int key) {
return key % size;
}
ostream& operator << (ostream& ostr , const HashTable& tbl ) {
for (int i=0; i<tbl.size; i++){
if ( tbl.hashTable[i] != NULL )
cout << i << " : " << *tbl.hashTable[i] << " ";
else
cout << "** ";
}
cout << endl;
return (ostr);
}
int menu () {
cout << "[1] insert value " << endl
<< "[2] find value " << endl
<< "[3] remove value " << endl
<< "[4] display table" << endl
<< "[5] exit " << endl
<< " >> ";
int choice;
cin >> choice;
return choice;
}
int main (int argc , char* argv[]) {
cout << "Enter Size of hash : ";
int size , key;
cin >> size;
//
HashTable hashTable(size);
//
time_t aTime;
srand( static_cast<unsigned>(time(&aTime)));
for (int i=0; i<size/2; i++)
hashTable.insert( rand() % (100*size) );
//
bool state = true;
while ( state ) {
switch (menu()) {
case 1 :
cout << "Enter key to insert: ";
cin >> key;
hashTable.insert(key);
break;
case 2:
cout << "Enter key to find: ";
cin >> key;
if ( hashTable.find(key) != NULL )
cout << "Found key " << key << endl;
else
cout << "cannot found " << key << endl;
break;
case 3:
cout << "Enter key to remove : ";
cin >> key;
hashTable.remove(key);
break;
case 4:
cout << hashTable << endl;
break;
case 5 :
state = false;
break;
}
}
return (0);
}
خلاصة
- hash table من أسرع هياكل البيانات ويجب أستخدامها في حال أردت سرعه كبيره في عمليه البحث والإدخال ،،
- تستخدم هذه البنيه داله هاشيه hash function تقوم بتحويل المدخلات الى قيم محصوره تكون عباره عن مواقع Index في الجدول table .
- عند حصول التصادم يمكن حله باستخدام طريقه الopen addressing أو طريقه الSeparate Chaining ، في حال أستخدمت الطريقه الأولى فطريقه الDouble Hashing هي الأفضل ما عدا في حاله كان الجدول لا يتغير ولا توجد فيه عمليات ادخال بعد انشائه فيمكن استخدام Linear hashing ، الطريقه الثانيه Separate Chaining هي الأفضل بشكل عام من طرق open addressing حيث هي غير متعلقه بالLoad facotr ، كما أننا يمكن أن نجري أي عمليات على الجدول بعد انشائه بكل سهوله ،،
في هذا الرابط نفس البرامج الموجودة في المقالة ولكن بلغه الجافا
تمرين
عمل Spell Checker باستخدام الHash Table
لديك في هذا المجلد (قم بتحميله من هنا) الملف dict.txt يحتوي على 25000 كلمه ،، ولديك ملف أخر example.txt يحتوي على فقره بها بعض الكلمات الخاطئه ، المطلوب هو تطوير برنامج يقوم بطباعه الكلمات الخاطئه على الشاشه ،، ويمكنك أن تطلب من المستخدم اعاده ادخالها مره أخرى وبعد ذلك قم بحفظ التعديل في الملف example.txt ..
المصدر Reference
Teach yourself data structure in 21 days