خوارزمية Sieve of Eratosthenes

تعتبر خوارزمية Sieve of Eratosthenes من أسهل الخوارزميات لإيجاد الأعداد الأولية Prime Numbers ضمن مجال معين من الأعداد الصحيحة n ، حيث تقوم فكرتها على حذف مضاعفات الأعداد داخل هذا المجال ، حيث أن تعريف الأعداد الأولية يستبعد وجود الأعداد التي يمكن إيجادها كحاصل ضرب عددين.

الخوارزمية من wikipedia

1. Create a list of consecutive integers from two to n: (2, 3, 4, ..., n).
2. Initially, let p equal 2, the first prime number.
3. Strike from the list all multiples of p greater than p.
4. Find the first number remaining on the list greater than p (this number is the next prime); let p equal this number.
5. Repeat steps 3 and 4 until p^2 is greater than n.
6. All the remaining numbers on the list are prime.

سنوضح الخوارزمية عبر مثال بسيط لإيجاد الأعداد الأولية من 1 إلى 100.
(ملاحظة: العدد 1 لا يعتبر عدد أولي حيث أنه لا يوجد عددين مختلفين يقسما العدد 1) :

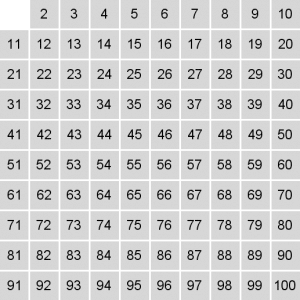
في البداية سننشئ مصفوفة من الأعداد :

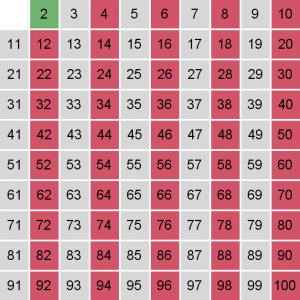
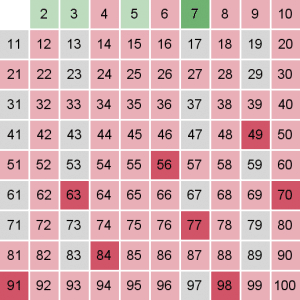
سنبدأ من العدد الأولي 2 ، وسنقوم بإزالة كل مضاعفاته ابتداءا من 4 :

ملاحظة: اللون الاخضر يعني عدد أولي ، أما الأحمر فهو ليس أولي.

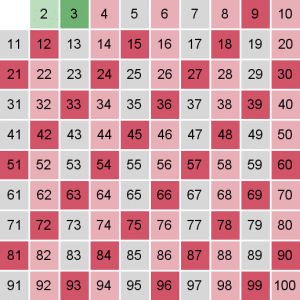
العدد 3 هو أولي ، وسنحذف كل مضاعفاته ابتداءا من 9 :

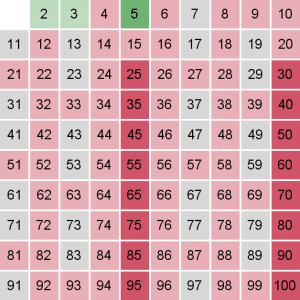
نفس الفكرة مع العدد 5 :

وكذلك العدد 7:

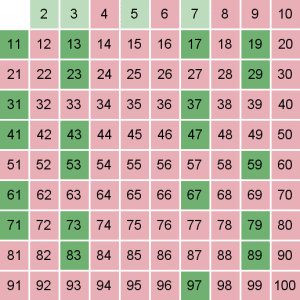
العدد التالي الآن هو 11 ، لكن سنتوقف هنا لأن مربع العدد 11 أكبر من المجال المطلوب 100.

إذاً الأعداد الأولية من 1 إلى 100 هي :

مثال آخر :

الصورة متحركه قم بالضغط عليها لمشاهدتها

تطبيق الخوارزمية :

هذا تطبيق بسيط للخوارزمية باستخدام سي++ ، والفكرة مشابهة تماما للمثال في الأعلى حيث سأنشئ مصفوفة من 100 عنصر ، وسأضع جميع القيم فيها مساوية للواحد دلالة على أن كل العناصر هي أولية ، وبعدها عندما نجد عدد مركب Composite number وليكن i سنجعل قيمة العنصر i هي الصفر دلالة على أنه تم حذف العنصر.

#include
#include
#include

using namespace std;

void sieveOfEratosthenes(int N)
{
    int *array = new int[N + 1];

    for (int i = 2; i <= N; ++i)
        array[i] = 1;

    array[1] = 0;

    for (int i = 2; i <= sqrt(N); ++i)
    {
        if (array[i] == 0)
            continue;
        for (int j = i * i; j <= N; j += i)
        {
            array[j] = 0;
        }
    }

    for (int i = 2; i <= N; ++i)
        if (array[i])
            cout << i << " ";

    cout << endl;
    delete[] array;
}

int main(int argc, char *argv[])
{
    if (argc == 2)
        sieveOfEratosthenes(atoi(argv[1]));
    else
        sieveOfEratosthenes(100);

    return 0;
}

شرح بسيط :

int *array = new int[N + 1];

for (int i = 2; i <= N; ++i)
    array[i] = 1;

array[1] = 0;

هنا تم انشاء المصفوفة وتعيين القيمة 1 لكل الأعداد دلالة على أنها أولية ، أما العدد 1 فتم تعيين القيمة 0 له دلالة على أنه ليس عدد أولي.

for (int i = 2; i <= sqrt(N); ++i)
{
    if (array[i] == 0)
        continue;
    for (int j = i * i; j <= N; j += i)
    {
        array[j] = 0;
    }
}

لا يوجد داعي لأن نمر على جميع الأعداد من 1 الى 100 ! سنبدأ من العدد 2 لأن العدد 1 قد ذكرنا بأنه ليس أولي ، وسننتهي عند العدد 10 (تأتي من تطبيق الجذر التربيعي على n) لأنه عنما تعمل الخوارزمية على العدد 2 و 3 و 5 و 7 و9 ستجد أننا قد مررنا على كل الأعداد (المضاعفة) في هذا المجال.

في البداية سيتم اختبار هل العدد ليس أولي ؟ إذا كانت الاجابة لا فهذا يعني أن العدد أولي ويجب معرفة مضاعفاته لكي نقوم بازالتها .
أما إذا كانت الإجابة نعم فهذا يعني أن هذا العدد مضاعف Composite number وبالتأكيد مضاعفات هذا العدد هي ليس أولية وقد تم ازالتها من قبل.

نتيجة البرنامج :
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

وهذا تطبيق آخر للدالة :

void sieveOfEratosthenes(int N)
{
    int *array = new int[N + 1];

    for (int i = 2; i <= N; ++i)
        array[i] = 1;

    array[1] = 0;

    for (int i = 2; i <= N / 2; ++i)
        for (int j = 2; j <= N / i; ++j)
        {
            cout << i * j << endl;
            array[i * j] = 0;
        }

    for (int i = 2; i <= N; ++i)
        if (array[i])
            cout << i << " ";

    cout << endl;
    delete[] array;
}

مصادر:
Wikipedia
Prime_number
Sieve_of_Eratosthenes
كتاب Algorithms in C.

الكود بالمرفقات.
printprime.cpp.tar