خوارزميات مطابقة النصوص Pattern Matching Algorithm

خوارزميات مطابقة النصوص Pattern Matching أو البحث في النصوص من المواضيع المهمه في مجال الخوارزميات ، حيث الهدف هو البحث عن نص ما سوف نطلق عليه Pattern داخل مجموعه كبيره من النصوص Text ـ ويمكن أن يكون البحث عن النمط بالضبط exact او عن أي نمط قريب للنمط المراد البحث عنه ، وبما أن خوارزميات البحث المتسلسل Linear Search والبحث الثنائي Binary Search تستخدم في البحث عن “مفتاح واحد” داخل مجموعه كبيره من النصوص (أو الأرقام)  فإنها لا تصلح استخدامها في حالتنا هذه ، فنحن نريد البحث عن نمط معين (مجموعه من المفاتيح أو الحروف ) داخل النص الكبير وليس مفتاح واحد فقط وأحيانا نريد البحث عن أي نمط أخر مشابه.

أنواع خوارزميات مطابقة النصوص

خوارزميات المطابقة مهمه للغايه لأي مبرمج، حيث أن تطبيقات موضوع بحث النصوص كبيره ومتنوعه، مثلا أغلب برامج محررات النصوص توجد فيها خاصيه بحث وأستبدال Find and Replace هل تسأئلت يوما كيف تجري هذه العمليه وما هي الخوارزميه المستخدمه ؟ -أغلب البرامج تستخدم خوارزميه Boyer-Moore algorithm  – حيث تقوم هذه الخوارزمية بالبحث عن جميع الكلمات في الملف لكي تستبدل النص الجديد بجميع النصوص المشابه للنمط المراد البحث عنه.  هذه الخوارزمية Boyer-Moore وغيرها من الخوارزميات التي تبحث عن النص المشابه تسمى Exact String Searching وهناك حوالى 20 خوارزميه أو أكثر.

نوع أخر من الخوارزميات المطابقة وهي البحث عن طريق أول مجموعه من الأحرف فقط ، وأقرب مثال يوضح فائدته هو أن يكون لدينا قاعده بيانات ضخمه لجميع هواتف المواطنين ، ونريد البحث عن رقم أي مواطن بإسم “محمد أحمد” بالطبع استخدام خوارزميه تعمل بمبدأ البحث اسم بأسم في هذه الحاله غير مجدي بتاتا خصوصا في حاله كان القاعده كبيره جدا  (عشرات ال gigabyte)  ولذلك سوف نوع من أنوع الأشجار B-Tree ونرتب فيها البيانات (لكي نحمل الإسماء من الملف الى الذاكرة) وبعدها نجري عمليه البحث باستخدام خوارزمية ال Prefix Searching، مثال أخر على هذه الخوارزميات وهو في البحث عن نمط ناقص، لنفرض أنك شاهدت حادث ما في الطريق وأستطعت أن ترى أول رقمين في لوحه السياره ولم تستطع معرفه الثالث الأن باستخدام خوارزميات المطابقه (Prefix Searching) تستطيع بكل سهوله وسرعه ايجاد جميع الأرقام التي تبدأ بهذه الرقمين ، مثال أخر على تطبيق هذا النوع من البحث prefix searching وهو في محرك البحث Google حيث لديه ميزه جميله وهو أنك بمجرد كتابه الكلمه الأولى في المحرك فيقوم بعرض جميع الكلمات التي تبدأ بهذا الأسم ،وأيضا خوارزميات prefix searching تستخدم في شريط عنوان المتصفح Firefox.

نوع أخر من الخوارزميات تستخدمه برامج الأنتي فايروس حيث تقوم بالبحث عن التوقيع في قاعده بيانات تحتوي على الألاف التواقيع في مده صغيره جدا قد لا تتجاوز ثانيه واحده وتحتاج الى خوارزميات للبحث عن أكثر من نمط في المره الواحده Multiple pattern searching مثل خوارزمية Aho-Corasick حيث في هذا النوع سوف تستخدم الأشجار Tree كهيكل للبيانات أو الأصح شجرة ال ternary Search Tree والتي تم الحديث عنها هنا، حيث البحث في الأشجار سريع جدا مقارنه مع غيره،  او حتى تستخدم بنيه Hash Table (سبق الحديث عنها هنا) مثل طريقة Veld man.

الأمثله على التطبيقات في مطابقه النصوص لا تنتهي ويمكن أن تدمج هذه الخوارزميات وخوارزميات أخرى لتكون لدينا مشاريع رائعه للغايه وعمليه أيضا ، فمثلا يمكن عمل برنامج لكشف الغش في الأختبارات، حيث يقوم البرنامج باستقبال اجابات طالبين ومن ثم يقوم بتظليل جميع الكلمات المتطابقه وفي النهايه يعرض تقرير يوضح عدد الكلمات المتطابقه وفي حال زاد العدد عن عدد معين ، فنستنتج أن الطالبين غاشين . مثال أخر وهو المحرر الأملائي في برامج محررات النصوص ، حيث أنك بمجرد كتابه الكلمه فيقوم الجزء المسؤول عن التأكد من الأخطاء (عادة هو Thread أخر يعمل بمجرد بدء البرنامج ) بالبحث في القاعده التي تحتوي على جميع الكلمات في اللغه العربيه فاذا وجد أنها موجوده فهذا يعني أن الكلمه صحيحه ، والا فيقوم بعرض جميع الكلمات القريبه ويكون هذا باستخدام خوارزميات لايجاد النصوص الأقرب للنمط وذلك بالأعتماد على طريقه نطقها Sound وأشهر خوارزميات هذا النوع هو Soundix Searching.

الخوارزمية Naive Searching Algorithm

تعريفات: عندما يتم ذكر مصطلح النمط أو Pattern فهذا يعني النص الذي نريد البحث عنه، وعندما يتم ذكر النص الكبير أو Text فنحن نقصد النص الذي يحتوي على جميع الحروف .

نبدأ الأن في أحد أقدم وأبسط الخوارزميات وفكرتها تكون عن طريق مقارنه حرف من ال pattern مع حرف مع ال Text، فاذا تطابق الحرفين ، فنقوم بالذهاب الى الحرف التالى في كل من النمط pattern وال text. اما في حال لم يتطابقا فنقوم بتحريك مؤشر الحرف في ال text الى الحرف التالي ونقوم بارجاع مؤشر الحرف في pattern الى البدايه ، وسوف نبدأ عمليه المقارنه مره أخرى . وسوف نستمر هكذا الى أن نجد التطابق في كل حروف ال pattern، أو أن نصل لنهايه ال text. وسوف نشير الى طول ال pattern بالحرف M أما طول ال text سوف نشير له بالحرف N. وسوف نتوقف في البحث عندما نصل ل N-M لأننا عندما نصل لتلك الخانه وحتى اذا كان الحرف التالي متطابق فسوف نتوق ف لأن ال Text سوف يكون أصغر من ال pattern.

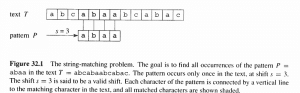
الصوره التاليه توضيح عمليه البحث عن النمط abaa ، حيث تمت مقارنه الحرف الأول في النمط مع الحرف الأول من الtext وكانت النتيجه صحيحه ، وسيتم الانتقال الى الحرف التالى في كل من text وpattern .  وهنا عندما تتم المقارنه فالنتيجه غير صحيحه وبالتالى نحرك مؤشر ال text للأمام ، ونرجع ال pattern للبدايه ، ونبدأ البحث مره أخر. لاحظ عدد مرات الshift هي 3 مرات حيث توصلنا للموقع الحرف المطابق في ال Index ثلاثه .

الشكل يبين خوارزمية ال Naïve Search

والصوره التاليه توضح الخوارزميه بشكل بسيط ، ويمكن أن تطبقها باللغه التي تريد:

الشكل يبين ال Pseudo code للخوارزمية

هناك من طبق الخوارزميه بأكثر من وجه ولكنها في النهايه هي نفس النتيجه ، الكود التالى يوضح لنا تطبيق الخوارزميه بعده طرق ممكنه (قد يصعب تتبع مثل هذه الحلقات لذلك لا أفضل من الورقه والقلم في حال لم تستطيع فهم الحلقه بشكل جيد).

كود سي++ لتطبيق خوارزمية Naïve Search

// implement Naive String Search (also known as Brute-Force) Using Several Method
// By : Wajdy Essam

#include <iostream>
using std:: string ;

// C implementation
// return the first index when match string
int BruteForceSearch1 (char* pattern , char* text) {
   int i , j , m = strlen(pattern) , n = strlen(text) ;

   for (i=0 , j=0 ; j<m && i<n ; i++,j++ ) {
      while ( pattern[j] != text[i]) {
         i -= j-1 ;
         j = 0 ;
      }

      if ( j == m )
         return i-m ;
      else
         return i ;
   }
}

// C implementation
// printing index for all matching string in text
void BruteForceSearch2 (char* pattern , char* text ) {
   int i , j , m = strlen(pattern) , n = strlen(text) ;

   for (j=0 ; j<=n-m ; j++) {
      for (i=0 ; i<m && pattern[i] == text[i+j] ; i++)  ;    // note ; here
      if ( i >= m)
         std::cout << j << " " ;
   }
}

// C++ Implementation
// return first index when mathc string , else return -1 
class NaiveSearch {
   public :
      NaiveSearch() { mText = "" ;}
      NaiveSearch(const string& text) : mText(text) {  }

      bool matchAt (const string& pattern , int position) const {
         for (int i=0 ; i<pattern.length() ; i++) {
            if ( pattern[i] != mText[i + position] )
               return false ;
         }

         return true ;
      }

      int match (const string& pattern) const {
         for (int i=0 ; i+pattern.length() < mText.length() ; i++)
            if ( matchAt(pattern,i) )
               return i ;

         return -1 ;
      }
   private :
      string mText ;
};

int main (int argc , char* argv[]) {
   // test first method
   std:: cout << "index is : " << BruteForceSearch1("ss","wajdy essam is assembly programmer") << std::endl ;

   // test second method
   std:: cout << "index is : " ;  BruteForceSearch2("ss","wajdy essam is assembly programmer");
   std::cout<<std::endl;

   // test third method
   NaiveSearch ns("wajdy essam is assembly programmer");
   std:: cout << "index is : " << ns.match("ss");

   return (0) ;
}

كود جافا لتطبيق خوارزمية Naïve Search

// Java Implementation for Naive Search Algorithm

public class Demo{
   public static void main (String args[]) {
      // test first method
      System.out.println("Index is : " + BruteForceSearch1("ss","wajdy essam is assembly programmer") ) ;

      // test second method
      System.out.print("index is : ") ;  BruteForceSearch2("ss","wajdy essam is assembly programmer"); 
      System.out.println();

      // test third method
      NaiveSearch ns = new NaiveSearch("wajdy essam is assembly programmer");
      System.out.println("index is : " + ns.match("ss") );
   }

   // return the first index when match string
   static int BruteForceSearch1 (String pattern , String text) {
      int i , j , m = pattern.length() , n = text.length()  ;

      for (i=0 , j=0 ; j<m && i<n ; i++,j++ ) {
         while ( pattern.charAt(j) != text.charAt(i) ){
            i -= j-1 ;
            j = 0 ;
         }

         if ( j == m )
            return i-m ;
         else
            return i ;
      }

      return -1 ;
   }

   // printing index for all matching string in text
   static void BruteForceSearch2 (String pattern , String text ) {
      int i , j , m = pattern.length()  , n = text.length()  ;

      for (j=0 ; j<=n-m ; j++) {
         for (i=0 ; i<m && pattern.charAt(i) == text.charAt(i+j) ; i++)  ;    // note ; here

         if ( i >= m)
            System.out.print(j + " ");
      }
   }
}

// return first index when mathc string , else return -1 
class NaiveSearch {
   public NaiveSearch() { mText = "" ;}
   public NaiveSearch(String  text) { mText = text ; }

   public boolean matchAt (String pattern , int position) {
      for (int i=0 ; i<pattern.length() ; i++) {
         if ( pattern.charAt(i) != mText.charAt(i+position) )
            return false ;
      }

      return true ;
   }

   public int match (String pattern)  {
      for (int i=0 ; i+pattern.length() < mText.length() ; i++)
         if ( matchAt(pattern,i) )
            return i ;

      return -1 ;
   }

   private String mText ;
}

هذه الخوارميه غير جيده وذلك لأنها تقوم بمقارنه كل حرف مع الحرف الأخر ، وفي حال لم يتطابقا سوف تعيد عمليه المقارنه لجميع حروف الpattern مع الحرف التالي من النص ، فاذا كان طول النص عدد N و والpattern  عدد M فسوف يكون ال  Big-O لهذه العمليه هو   N*M

الخوارزمية Knuth – Morris – Pratt String Matching

في عام 1977 نشر الثلاثي  Knuth (صاحب كتاب Art of programming الشهير) و Morris و Pratt مقاله Fast Pattern Matching in Strings  وتحدثوا فيها عن ايجاد خوارزميه أسرع من الطريقه التي تعتمد على Brute-Force  وسميت هذه الخوارزميه بأسم هؤلاء الأشخاص وأختصارا KMP .

للننظر قليلا الى ال Brute-Force وسنجد أنها عندما تجد حرف في pattern لا يطابق الحرف في text فإنها تقوم بالذهاب الى الحرف التالي من الtext  وتعيد المقارنه من أول الPattern .  خوارزميه KMP جائت لتحسين تلك الخوارزميه حيث تم التخلص من عمليات المقارنه المتكرره، طريقه عملها كالتالي:

أولا تقارن الحرف الأول في الpattern  مع الحرف الأول من ال text في حاله كانا مختلفين فتقوم بالذهاب الى الموقع التالى من text ( كما في Brute-Force بالضبط) ولكن الأختلاف يكون في حال قمنا بمقارنه ثلاثه حروف من الtext  مع ال     pattern وكانت النتيجه صحيحه ولكن الحرف الرابع يختلف ، هنا في هذه الحاله لن نقوم كما في الbrute-force  باعاده مقارنه جميع الحروف مع الحرف التالى من text ، لكن بما أننا نعلم بأن هذه الحروف قمنا بمطابقتها سابقا فنقوم بالذهاب الى الموقع التالى من text الذي يشابه هذه الحروف التي طابقناها . وبالتالى ستكون هناك عمليات أقل وبالتالى الخوارزميه أسرع بكثير من السابقه.

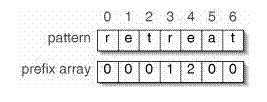
في البدايه يجب أن نقوم بحساب Prefix للpattern  وسوف نحتاجه عندما نقوم بمقارنه الpattern  مع text ، حيث هذه prefix array  تحتوي على عدد الأحرف المشابه من أول الpattern  للحرف الحالى من الpattern ، الصوره التاليه توضح كيف يمكن حسابه :

الشكل يبين كيف يمكن حساب ال Prefix Array

لاحظ في الصوره الموقع 3 (الحرف r) يحتوي على 1 والسبب أن الحرف r موجود في الموقع 0 . 1 تشير الى عدد الأحرف الprefix . أيضا الموقع التالى 4 (الحرف e) يحتوي على 2 والسبب أن الحرفين في الموقعين 0و1 مشابهين للحرفين في الموقع 3و4.  يعني الprefix  تعني اذا كانت هناك عدد n من الحروف من أول الpattern  مشابه لعدد n من الحروف في الحرف الحالى من ال pattern اذا نقوم بكتابه ذلك العدد n في الprefix array .

مثال أخر :

الشكل يبين كيف يمكن حساب ال Prefix Array

كما ذكرنا هذه الprefix arrayسوف نستخدمها في خوازرميه البحث عندما لا يتطابق الحرف من pattern مع الحرف من الtext وبالتالي يتم الرجوع الى الخانه المكتوبه في الPrefix array وبالتالى سوف نتجنب عمليه المقارنه للأحرف التي قمنا بها .

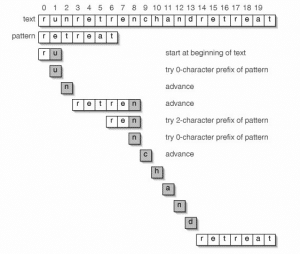
الشكل التالي يوضح كيفية البحث عن ال pattern في ال text:

الشكل يبين كيفية البحث عن النمط في النص الأصلي

نبدأ شرح طريقه عمل الخوارزميه (البحث) ، أول نقارن الحرف الأول من الpattern  مع الحرف الأول من ال text فنجد أنهما متطابقان ، نقوم بالذهاب الى الحرف التالى في كل من ال pattern والtext . نختبر وسنجد أن الحرفين غير ذلك ،، اذاً في هذه الحاله سوف يكون الرقم الموجود في الخانه الأولى في الprefix array  ونبدأ منه (وهو في الحاله 0) ، اذاً سبندأ نختبر مره أخرى من الحرف r . سنختبره مع u وسنجد أنهم غير متساوين ، مره أخرى نختبره مع الحرف التالى n ونجد أنهما غير متساوين ثم نختبره مره أخرى مع r وسنجد أنهما متساوين ، نختبر الحرف التالي في كل من pattern والtext  وسنجد أن الحروف e و t و r و e متطابقين ، نذهب للحرف التالى وهو a في ال pattern و n في الtext ، نقوم بالأختبار وسنجد أنهم غير متساوين ؟ اذاً نقوم بالذهاب الى الرقم الموجود في الخانه match-1  (المتغير match يشير الى Index الحرف في الpattern)  في   prefixarray وهو 2 ، ونقوم بالأختبار مره أخرى الحرف t من الpattern  مع الحرف n من الtext  ؟ سنجد أنهم غير متطابقين ، سنذهب الأن الى الخانه match-1 في ال prefixArray وهو هنا 0 أي الحرف r ، وسنقوم باختباره مع الحرف n في text ؟ والنتيجة غير متطابقين ، وسوف نقوم بالذهاب الى الحرف التالى وهو c وسنجد أنه غير كذلك ، نذهب للحرف التالى والتالى الى أن نصل للحرف r . وسنختبر وسنجد التطابق للحرف r وما بعده .

الكود التالي تطبيق لخوارزمية KMP بلغه سي++

// C++ Implementation , Wajdy Essam
// Knuth - Morris - Pratt Algorithm

#include <iostream>
using namespace std ;

class KMP {
   public :
      KMP () : mText("") , mPattern("") { }
      KMP (const string& txt) : mText(txt) , mPattern("") { }
      KMP (const string& txt, const string& pattern) : mText(txt),mPattern(pattern) { }

      int search()                            { return search(mText,mPattern) ; }
      int search(const string& pattern)             { return search(mText,pattern)  ; }

      int search(const string& text , const string& pattern) {
         int prefixArray[ pattern.length() ] ;

         initializeToZero(prefixArray,pattern.length());
         preProcessing(pattern,prefixArray);

         int i = 0 , match = 0 ;
         while ( i < text.length() ) {
            if ( text[i] == pattern[match]  )  {
               match++ ;
               if ( match == pattern.length() )
                  return i + 1 - pattern.length() ;
               else
                  i++ ;
            }
            else if ( match > 0 )
               match = prefixArray[match-1];
            else
               i++;
         }

         return -1 ;
      }

   private :
      void initializeToZero (int* next,int count) {
         for (int i=0; i<count ; i++)
            next[i] = 0 ;
      }

      void preProcessing (const string& pattern , int* next ) {
         int i=1 , match = 0 ;

         while ( i < pattern.length() ) {
            if ( pattern[i] == pattern[match] ) {
               match++;
               next[i] = match ;
               i++;
            }
            else if (match > 0 ) 
               match = next[match-1] ;
            else
               i++;
         }
      }

   private :
      string mText ;
      string mPattern ;
};

int main (int argc , char* argv[]) {
   KMP kmp("aaabaaaabaaaaab");
   cout << "Find (aaaaa) At index : " << kmp.search("aaaaa") << endl;

   return (0);
}

وكود جافا لتطبيق خوارزمية KMP:

// Java Implementation
// Knuth - Morris - Pratt Algorithm

class JavaKMP {
   public static void main (String args[]) {
      JavaKMP kmp = new JavaKMP("aaabaaaabaaaaab");
      System.out.println("Find (aaaaa) At Index : " + kmp.search("aaaaa") );
   }

   public JavaKMP ()                      { mText = ""  ; mPattern = ""      ; }
   public JavaKMP (String txt)             { mText = txt ; mPattern = ""      ; }
   public JavaKMP (String txt, String pattern) { mText = txt ; mPattern = pattern ; }

   public int search()                   { return search(mText,mPattern)    ; }
   public int search(String pattern)          { return search(mText,pattern)     ; }

   public int search(String text , String pattern) {
      int prefixArray[] = new int[pattern.length()];

      initializeToZero(prefixArray,pattern.length());
      preProcessing(pattern,prefixArray);

      int i = 0 , match = 0 ;
      while ( i < text.length() ) {
         if ( text.charAt(i) == pattern.charAt(match)  )  {
            match++ ;
            if ( match == pattern.length() )
               return i + 1 - pattern.length() ;
            else
               i++ ;
         }
         else if ( match > 0 )
            match = prefixArray[match-1];
         else
            i++;
      }

      return -1 ;
   }

   private void initializeToZero (int next[],int count) {
      for (int i=0; i<count ; i++)
         next[i] = 0 ;
   }

   private void preProcessing (String pattern , int next[] ) {
      int i=1 , match = 0 ;

      while ( i < pattern.length() ) {
         if ( pattern.charAt(i) == pattern.charAt(match) ) {
            match++;
            next[i] = match ;
            i++;
         }
         else if (match > 0 ) 
            match = next[match-1] ;
         else
            i++;
      }
   }

   private String mText ;
   private String mPattern ;
}

الخوارزمية Boyer-Moore Algorithm

نتحدث هذه المره عن أحد أسرع الخوارزميات المستخدمه في عمليه البحث عن النصوص وهي Boyer-Moore وسميت بذلك بالطبع نسبه لمخترعي هذه الخوارزميه حيث قدموها في عام 1977 كبديل للطريقه البحث البدائيه أو ما يسمى ب Naive Searching.

المقارنه في هذه الخوارزميه تعتمد على البدء من اليمين الى اليسار وليس كما هو الحال مع الخوارزميات العاديه ،، بالاضافه الى انها تقلل كثيرا من عمليات المقارنه خصوصا في حال لم يكن الحرف في text موجود في الـ pattern حيث تقفر بمقدار معين نقوم بحسابه كما سيتبين الأن ، هذا المقدار سوف يكون في جدول الازاحه skip ( أو بالأسم الصحيح  Bad-Character Shift) بمعنى أن هناك عمليه تحليل للـ pattern قبل البدء في البحث ، كما هو الحال مع KMP.

جدول الإزاحه يجب أن يكون حجمه مساوي لحجم ال character set التي نريد أن يتكون منها النص text والنمط pattern، وبما أننا حاليا سوف نبحث عن الحروف الأنجليزيه سوف يكون حجم الجدول بعدد حروف ال ASCII وهي 256 . وقبل أن نبدأ في البحث في النص ، يجب أن نقوم بتحليل النمط ونقوم بتعبئه الحرف المقابل في الجدول للحرف المقابل للنمط بمقدار ظهور أخر index للنمط .

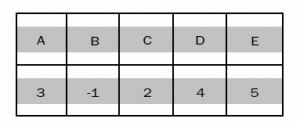
المثال التالي يوضح لنا كل شيء ، لنفرض لدينا الcharacter set  مكونه من الحروف A,B,C,D,E والنمط هو DECADE ، سوف يكون شكل الجدول كالتالي :

الشكل يبين جدول الإزاحة

تم حساب هذا الجدول كالتالي ، نبدأ من اليسار لليمين ونقوم بوضع ال Index لكل حرف في الpattern  في الجدول .أولاً D موقعه هو 0، وسنضع 0 في الخانه المناسبه للحرف D في الجدول(الخانه الثالثه -الترقيم من 0-). ثانياً الحرف E موقعه هو 1 وسنضع 1 في الخانه المناسبه للحروف E في الجدول .وسنستمر كذلك.

لاحظ أن الحرف D سيتكرر مره ثانيه وسنقوم بكتابه الIndex  الجديد (4) في الخانه القديمه ، وبنفس الأمر للحرف E. وهذا هو لب عمليه التحليل في البدايه ، فقط نحن نريد موقع أخر ظهور للحرف ، وهو ما سنحتاجه في عمليه البحث في حال أختلف الحرف من النص مع النمط .لاحظ أيضا بقيه الحروف في الcharacter set  والتي لا توجد لها قيم سنضع لها -1. الكود التالي يبين كيف يمكن حساب هذا الجدول:

هناك طريقه أخرى لعمل هذا الجدول حيث يتم تهيئه المصفوفه أولا بطول النمط ، سوف يتم وضح الحرف M-i-1 بدلا من i في الحلقه الثانيه ، وسوف تختلف عمليه البحث بشكل صغير أيضا ، لكن التطبيق أعلاه أسهل في الفهم والاستعياب من الثاني.

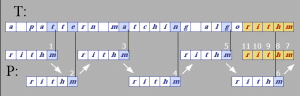
طريقه البحث في خوارزميه BM تكون كما توضح الصوره التاليه :

الشكل يبين طريقة البحث في خوارزمية BM

أولاً البحث كما ذكرنا في هذه الخوارزميه سوف يكون من اليمين لليسار بمعنى أول حرف سوف نبدأ به المقارنه هو الحرف i من text والحرف g من pattern . في حال لم يتساوى الحرفان والحرف i موجود في النمط سوف نقوم بتحريك النمط حرفين للأمام وهكذا يتطابق i مع i . وهكذا تطابقت الكلمتين .

نكمل لكي نوضح الحاله الثانيه في حال عدم التطابق وعدم وجود الحرف في النمط ، السطر التالي يقارن g من النمط مع ” ” مسافه من text ، وبما أنهم لا يتطابقان والحرف ” ” لا يوجد في النمط سوف نقوم بتحريك النمط بعدد حروف النمط
وهي 4 في حالتنا هذه (وهذا تحسين كبير جدا مقارنه مع البحث بالطريقه naive ) .

يمكن النظر للصوره القادمه وهي تبين كيف يتم البحث بشكل أوضح وأفضل :

الشكل يبين طريقة البحث في خوارزمية BM

كود تطبيق الخوارزميه  Boyer-Moore بسي++

// Boyer Moore String Searching

#include <iostream>
using namespace std ;

class BoyerMoore {
   public :
      BoyerMoore(const string& text) : mText(text)  { }
      BoyerMoore() : mText("") { }

      int match (const string& pattern ) {
         int skipTable[256]; 
         setSkipTable(pattern,skipTable);

         int s = 0;
         while (s <= mText.length() - pattern.length()) {
            int i = pattern.length() - 1;

            char c = 0;
            while (i >= 0 && pattern[i] == (c = mText[s+i])) {
               --i;
            }

            if (i < 0) {
               return s ;
            }

            s += max(i - skipTable[c], 1);
         }

         return -1 ;
      }

   private :
      void setSkipTable (const string& pattern, int* skipTable) {
         for (int i=0 ; i<256 ; i++)
            skipTable[i] = -1 ;

         for (int i=0 ; i<pattern.length() ; i++)  
            skipTable[pattern[i]] = i ;
      }

   private :
      string mText ;
};

كود تطبيق الخوارزمية Boyer-Moore بجافا:

// Java Implementation for BM

public class JavaBM {
   public static void main (String argc[]) {
      JavaBM bm = new JavaBM("String Seraching in Boyer Moore Algorithms");
      System.out.println("Find Index At : " +  bm.match("oor") );
   }

   private String mText ;

   public JavaBM (String txt) {  mText = txt ; }
   public JavaBM () { mText = "" ; }

   public int match (String pattern ) {
      int skipTable[] = new int[256] ;
      setSkipTable(pattern,skipTable);

      int s = 0;
      while (s <= mText.length() - pattern.length()) {
         int i = pattern.length() - 1;

         char c = 0;
         while (i >= 0 && pattern.charAt(i) == (c = mText.charAt(s+i))) {
            --i;
         }

         if (i < 0) {
            return s ;
         }

         s += Math.max(i - skipTable[c], 1);
      }

      return -1 ;
   }

   private void setSkipTable ( String pattern, int skipTable[] ) {
      for (int i=0 ; i<256 ; i++)
         skipTable[i] = -1 ;

      for (int i=0 ; i<pattern.length() ; i++)  
         skipTable[pattern.charAt(i)] = i ;
   }
}

ملاحظه :الخوارزميه الأصليه BM تحتوي بالاضافه على جدول Bad character heuristic على جدول أخر Good suffix heuristic وهو يحتوي أيضا على عدد مرات الإزاحه ولكن هذه المره للحروف المتطابقه ، على العموم الكثير من المقالات تحدثت حول أمكانيه ازاله هذا الجزء من الخوارزميه وتبقى بنفس الكفائه تقريبا .. وهذا ما قمنا به في درسنا اليوم وهو simplified version for BM .

خاتمة

نصل لنهايه المقالة ، أرجوا أن تكون مفيدة للباحث في هذا المجال، ويمكن ان تحل التمرين التالي لتعزيز المفاهيم في هذا الموضوع. فكرته: نريد عمل تطبيق بسيط نستفيد منه من هذه الخوارزميه ، مثلا نقوم بعمل محرر نصوص صغير جدا ، يحتوي فقط على مربع نص text area ويوجد زر اسمه find & replace نقوم فيه بكتابه الاسم المراد البحث عنه والكلمه المراد تغييرها ،، ومن ثم نضغط بدء العمليه ،، أغلب محررات تستخدم BM لأنها الأفضل وهو ما سنطبقه أيضا .. يمكن التطبيق بأي لغه برمجه ..