ماذا تعرف عن الـ Ternary Search Tree

ال Ternary Search Tree (أشجار البحث الثلاثية) هي بنية بيانات تستخدم لحفظ واسترجاع النصوص بسرعه كبيرة ، كما أنها يمكن اجراء عمليات خاصه في البحث مثلا البحث عن أي كلمه لها النمط a??b وهو ما يعرف Pattern Matching With Wildcards ، بالاضافة الى امكانية البحث عن طريق أول عده أحرف من النص وهو ما يسمى Prefix Searching .

وهي مشابه لشجره البحث الثنائية Binary Search Tree في أن القيمه في كل عقدة تكون أكبر من القيمه الموجوده في الإبن الأيسر وأصغر من القيمه الموجودة في الإبن الأيمن ، ولكنها تختلف عنها في أنها لا تحتوي على القيم (النص) في العقده الواحده ولكن كل عقده سوف تحتوي على حرف واحد من النص وهذه العقده تحتوي على مؤشر للعقده التالية والتي تحتوي على الحرف التالي من النص وهكذا كل عقده تحتوي على الحرف وتحتوي على المؤشر للعقده التي تحتوي على الحرف التالي (وبسبب هذا المؤشر سميت ب Ternary Search Tree).

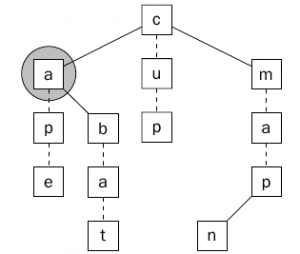
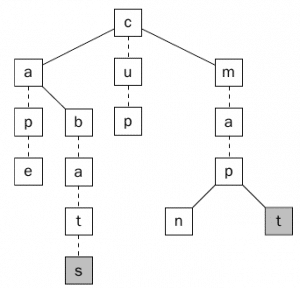
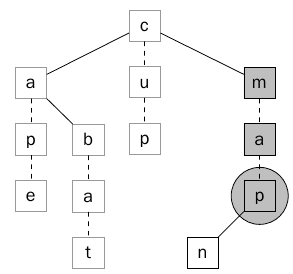
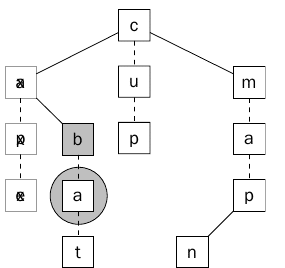
الشكل (1) يبين كيف يمكن حفظ الكلمات cup و ape و bat و man و map في الشجره Ternary Search Tree ، وأحرف الكلمة في الشجره تتصل بعلامه (شرطه – ) لكي يتم التفرقه بينهم وبين العقد الأبناء. وفي الشكل نجد أن العقد الملونه تشكل لنا المسار للكلمة bat.

الشكل 1 يبين Ternary Search Tree

في الشكل نجد أن العقده c هي الجذر root والإبن الأيمن m هو أكبر من ال c والإبن الأيسر a هو أصغر من ال c والعقدة b هي أكبر من a (كما في الأشجار الثنائية Binary Search Tree) . وكل من العقد الأبناء (التي تحتوي على رابط – ) سوف تحتوي على الحرف التالي من الكلمة ( الحرف a يأتي بعد b ويأتي بعده t وهكذا نصل للكلمة bat).

البحث عن الكلمة Searching for Word

في كل مستوي level في الشجره سيتم عمل بحث ثنائي Binary Search مع الحرف الأول من الكلمة التي يراد البحث عنها. والبحث مثل البحث في الBinary Search Tree حيث تكون البدايه من الجذر Root ويتم الإنتقال الى الإبن الأيمن أو الأيسر حسب الحرف المناسب وبعد أن يتم ايجاده يتم الأنتقال للمستوي level التالي ويتم بدء البحث مره أخرى ولكن بالحرف الثاني من الكلمة ويتم تكرار هذه الخطوات الى أن يتم ايجاد كل الحروف (وبالتالي يكون هناك تطابق) أو تنتهي العقد بدون حصول مطابقة.

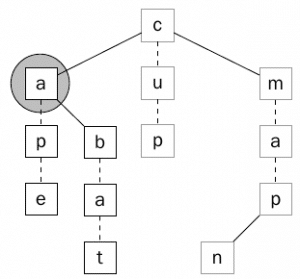
نعود للشكل الأول ونرى كيف يتم البحث عن الكلمة bat في تلك الشجره ويتم ذلك أولا من خلال مقارنه الحرف الأول مع الجذر c ولأن الحرف b أقل من c سيتم الإنتقال للإبن الأيسر كما يوضح ذلك الشكل التالي.

الشكل ‏2 يبين الإنتقال الى الإبن الأيسر

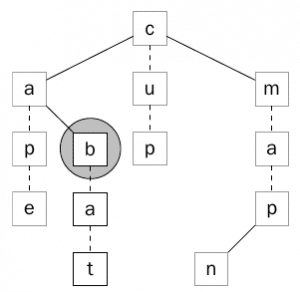
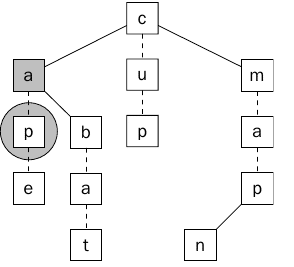
بعد ذلك سيتم عمل المقارنه مرة أخرى ويتم مقارنه الحرف الأول من الكلمة b مع الحرف a ونظراً لأن الحرف b أكبر سوف يتم الإنتقال للأبن الأيمن وهو b. كما يوضح ذلك الشكل (3).

الشكل ‏3 يبين الإنتقال للإبن الأيمن نظرا لأن الحرف b أكبر من العقده a

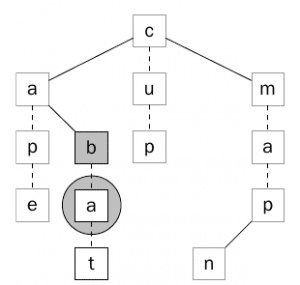
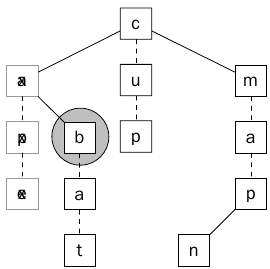
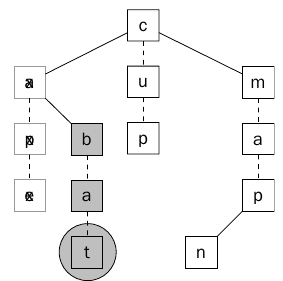
بعد ذلك سيتم عمل المقارنة مره أخرى وسيتم مقارنه الحرف b مع الحرف الأول من الكلمة وهو b وسيحصل تطابق وهكذا سيتم الإنتقال للأبن الأول للحرف b. كما يوضح ذلك الشكل (4).

الشكل ‏4 يبين أنه بعد التطابق يتم الإنتقال للأبن الأول من العقده التي حصل بها التطابق

بعد ذلك سيتم مقارنه الحرف الثاني من الكلمة مع الإبن الأول وسيحصل التطابق وبعدها تتم مقارنه الحرف الثالث t مع العقده التالية t وسيحصل التطابق وهكذا نكون قد تحصلنا على تطابق في 5 محاولات (مقارنات) ، كما يوضح ذلك الشكل (5).

الشكل ‏5 يبين توقف البحث بعد ايجاد أخر حرف من الكلمة

في كل مستوى يتم البحث عن الحرف بالبحث كما في Binary Search Tree وفي حال تم ايجاد الحرف يتم الإنتقال الى المستوى التالي ويتم البحث مره أخرى عن الحرف الثاني من الكلمة ويتم تكرار ذلك لجميع الأحرف في الكلمة من خلال ذلك يمكن معرفه زمن التشغيل Run-Time المستغرق للبحث عن الكلمة في الTernary Search Tree والتي في بعض الأحيان تكون أعلى كفائه من الBinary Search Tree.

لنأخذ مثال للبحث عن الكلمة man في الشجره السابقة ولنرى كم عدد المقارنات للبحث عن هذه الكلمة في الشجره Ternary Search Tree. أولا سوف نقارن الحرف c مع الحرف الأول من الكلمة وهو m وبما أنه أكبر سيتم الإنتقال للجهه اليمني (عدد المقارنات =1) سيتم مقارنه الحرف الأول m مع العقدة m وسنجد التطابق (عدد المقارنات=2) وسيتم الإنتقال للعقده التالية ويتم مقارنتها مع الحرف الثاني من الكلمة وهو a (عدد المقارنات=3( وسنجد أنهم متطابقان وسيتم الإنتقال للعقده التالية ويتم مقارنتها مع الحرف الثالث n وسنجد أنها غير متطابقه (عدد المقارنات=4) وهنا سوف نطبق البحث الثنائي Binary Search وسيتم الإنتقال للإبن الأيسر ويتم مقارنته مع الحرف n ويتم التطابق (عدد المقارنات=5).

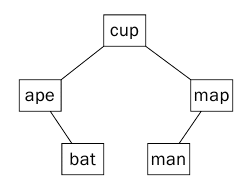
سوف نطبق البحث عن الكلمة man في شجره ثنائية Binary Search Tree ولنرى كم تكون عدد المقارنات في شجره البحث الثنائية والتي يوضحها الشكل (6) .

الشكل 6 يبين شجره بحث ثنائية Binary Search Tree

ستتم مقارنه الكلمة man مع الجذر cup ولن يتطابقا بعد أختلاف الحرف الأول في كل كلمة (عدد المقارنات=1) ، وسيتم الإنتقال للإبن الأيمن وتتم مقارنه map مع man وستتم مقارنه الحرف الأول في كل منهم (عدد المقارنات=2) وتحصل مطابقة ويتم مطابقة الحرف الثاني (عدد المقارنات =3) وتحصل مطابقة ويتم مطابقة الحرف الثالث n مع P ولن تحصل مطابقة (عدد المقارنات =4) لذلك سوف يتم الإنتقال للإبن الأيمن وسيتم اجراء 3 مقارنات ويحصل التطابق وبالتالي يكون مجموع المقارنات في شجره البحث الثنائية هو 7 مقارنات.

بالرغم من بساطة الشجره أعلاه الا أن المثال أوضح أن عمليات المقارنه في الTernary أقل من الBinary والسبب أن أي كلمات لها نفس الأحرف الإبتدائية تكون موضوعه مع بعض Compressed وبالتالي اذا تمت زياره هذه الأحرف فلن تحتاج اعاده الزياره لها مره أخرى بعكس الBinary Search Tree والتي تقوم بعمل مقارنه لكل الأحرف في أي عقدة في الشجره .

وبالإضافة الى كفائه الTernary Search على الBinary Search فالTernary لا تكمل البحث عند عدم المطابقة بأحرف أبتدائية Prefix Matching بينما في الBinary سوف تستمر بالبحث الى حين الوصول لأخر عقدة في الشجره.

لكي نعرف أداء الTernary Search Tree نفرض أن كل مستوى يحتوي على كل الأحرف الهجائية وتكون في شكل عقد (كما في الشجره الثنائية)، واذا كان عدد الأحرف في اللغه (من A الى Z ) هو M فإن عدد المقارنات في كل مستوى ستكون O(log M) لكل حرف ، وبالتالي لإيجاد كلمة بطول N سوف تكون عدد المقارنات O(N log M) وبشكل عملي سنجد أن الأداء أفضل من ذلك دائما بسبب خاصيه Common Prefix وأنه في الغالب لا تكون جميع أحرف الهجائية في كل مستوى.

إدخال الكلمات Inserting Words

ادخال الكلمات للشجره Ternary عملية سهله كما في البحث عن الكلمة ، فكل ما في الأمر هو اضافة عقدة جديدة Leaf Node لأي حرف لا يتواجد ، ونفرض أننا نريد أن ندخل الكملة bats في الشجره السابقة Ternary Search Tree فكل ما علينا هو اضافه الحرف s بعد الكلمة bat ، وفي حال كنا نريد أن نضيف الكلمة mat سوف نضيف العقدة t كأحد أبناء العقدة p. (بمعنى أن الأبناء التي روابطهم — سوف يكون أحد من هذه الأبناء هو الحرف التالي ، أما الأبناء التي روابطهم – فهم يكونوا الأحرف الأخرى ) .

الشكل (7) يوضح اضافه الكلمة bats والكلمة mat للشجره السابقة.

الشكل7 يبين اضافة الكلمة bats و mats وتمت اضافة عقدتين فقط

بعد اضافة تلك الكلمتين سنجد أن هناك كلمات الأحرف الإبتدائية لها متشابه has common prefix مثلا الكلمة bat و bats تبدأن ب bat . فهنا كيف يمكن أن نعرف أن كل من bat و bats تمثل كلمة وأن b و ba و ap ليست كلمات ؟

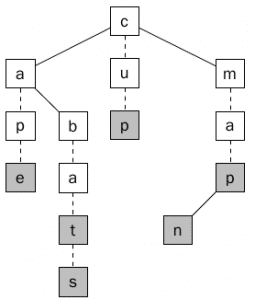
ويكون ذلك عن طريق اضافة علامة في أي عقدة تكون هي الحرف الأخير في الكلمة ، فيمكن أن نضيف متغير Boolean يحدد لي هل هذه العقده هي عقده أخيره في الكلمة أم لأ وفي حال كنا مثلا نريد تطبيق قاموس Dictionary فستكون هذه القيمه هي ترجمه الكلمة أو تعريفها. وبأي حال في النهايه نريد تطبيق علامه توضح لنا أن هذه العقده هي الأخيره في الكلمة ، كما يوضح ذلك الشكل (8) .

الشكل 8 يبين العقد (الملونه) التي تمثل الحرف الأخير في كل كلمة

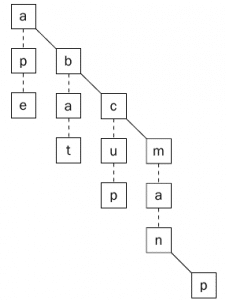
الشجره السابقة هي شجره متزنة Balanced Tree فكما أن الأشجار الثنائية يمكن أن تصبح غير متزنه Unbalanced فيمكن أن تصبح الTernary Search Tree أيضا غير متزنه. الشجره السابقة كانت متزنه والسبب أننا أدخلنا الكلمات بالترتيب التالي : Cup, ape, bat map, man ولكن في حال أدخلنا الكلمات مرتبة أبجديا أي بالترتيب: Ape,bat,cup,man,map سوف تكون الشجره غير متزنه ، كما يوضح ذلك الشكل (9).

الشكل ‏9 يبين شجره Ternary Search Tree غير متزنه

زمن البحث في الشجره المتزنه هي O(N log M) بينما في الشجره غير المتزنه يكون حوالي O(NM) وبشكل عملي وحتى لو لم تكن متزنه سوف يكون الأداء جيد بسبب تشارك الكلمات في بعض الأحرف الإبتدائية Prefix-Sharing بالإضافة الى أن كل مستوى لا توجد فيه جميع حروف اللغه.

Prefix Searching

أحد أهم أستخدامات الTernary Search Tree هي في البحث عن طريق مجموعه من الأحرف الإبتدائية وسيتم استخراج كل الكلمات التي تبدأ بهذه الأحرف والفكره تكون عن طريق البحث في Ternary Search Tree باستخدام هذه الPrefix (كما وضحناها سابقا في فقره البحث عن الكلمة) ، وبعد ذلك يتم زيارة الشجره بأسلوب In-Order والبحث عن العقده الأخيره (والتي تحتوي على علامة توضح بأنها نهايه الكلمة) في كل أبناء هذا الPrefix.

الزياره الIn-Order تكون مثل الزياره في الأشجار الثنائية Binary Search tree ولكن يجب زياره أبناء العقدة أيضا ، وعند انتهاء البحث بالطريقة التي وضحناها أعلاه والوصول لأخر عقدة في الPrefix ، نقوم بعد ذلك بالخطوات التالية:
• زياره الشق الأيسر left Subtree من العقدة.
• زيارة العقده نفسها.
• زيارة أبناء العقدة.
• زياره الشق الأيمن right Subtree من العقدة.

لنأخذ مثال للبحث عن الPrefix (ma) في الشجره السابقة ، وعند ايجاد هذا الPrefix سوف يتم اتباع الخطوات الأربعه السابقة حيث يتم أولا زياره الشجره الفرعيه اليسرى وسوف ترجع هذه الكلمة man وبعد ذلك يتم زياره العقدة نفسها ma ولكنها لا توجد بها علامة تدل على نهايه الكلمة وسنذهب للخطوه الثالثه وهو زياره ابناء العقدة اذا كان هناك أبناء وأخيرا سيتم زياره الشجره الفرعية اليمني ويتم ارجاع الكلمة map. الشكلين (10) و (11) يوضحوا تلك الخطوات .

الشكل ‏10 يبين ايجاد النهايه الأولى للma وهي man

الشكل ‏11 يبين ايجاد النهايه الثانية للكلمة ma وهي map

أثناء التجول Traverse في الشجره يمكن طباعه الكلمات التي يتم ايجادها أو جمعها واستخدامها بطريقة ما مثلا طباعتها في قائمه list للمستخدم.

Pattern Matching

أحد تطبيقات البحث باستخدام الTernary Search Tree هو البحث باستخدام أحرف غير معروفة وهذا ما يسمى الWildcard Searching فمثلا اذا أردنا البحث عن الكلمة التي تتكون من النمط a-r—t (الشرطه – هي الحرف الذي لا نعرفه وتسمى Wildcard) ويمكن أستخدام أي حرف لتمثيل الWildcard (مثلا . أو ? ) .

أحد أسهل الحلول لمطابقة نص للنص السابق a-r—t هو باستخدام الBrute-Force أي سيتم تجربة جميع الإحتمالات الممكنة بدءا من aaraaat وانتهاءا ب azrzzzt ولكن هذا الحل مستهلك للزمن والمصادر.

وبدلا من ذلك يمكن البحث بطريقة أفضل من خلال الشجره نفسها ، فيكون البحث بالطريقة العاديه وعند الوصول للحرف الWildcard (بالطبع لن نجد مطابق له في الشجره) سيتم زياره كل عقدة على أساس أنها هي ذلك الحرف.

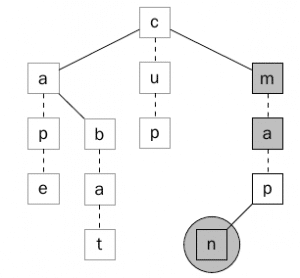
لنأخذ مثال على البحث عن النمط -a- في الشجره السابقة ، وكما في البحث العادي وسنبدأ من الجذر c والحرف الأول وهو – وبما أن هو Wildcard فسيتم تجربة كل عقده في المستوي الحالي بالترتيب. كما يوضح ذلك الشكل (12).

الشكل 12 يوضح أن استخدام الWildcard سوف يجعل البحث يبدأ بالترتيب من العقده الأولى

سوف يتم اختبار الحرف الثاني من النص a مع كل من أبناء العقدة a وسيتم مقارنه a مع الحرف p ولن يتطابقها (لا يتطابق –a مع –p ) لذلك سيتم تجاهل هذا المسار ويوضح ذلك الشكل (13) .

الشكل ‏13 يبين حرف غير مطابق وبالتالي يتوقف البحث في المسار الحالي

يتم النظر في بقية الأبناء اذا كان هناك للعقده a ، وهناك ابن الأخر للعقدة a سيتم البحث به كما يوضح ذلك الشكل (14).

الشكل 14 يبين زياره العقدة الثانية

مره أخرى ولأننا نبحث عن Wildcard سيتم افتراض أن الحرف الأول تمت مطابقته وننتقل للحرف الثاني من النص a وللعقده التالية.

الشكل 15 يبين تطابق والإنتقال للحرف التالي.

كما يوضح الشكل السابق سيكون هناك تطابق بين العقدة a والحرف a في النص ، ولكن هناك عده أحرف في النص يجب مطابقتها فيتم الإنتقال للحرف التالي والإبن التالي.

الشكل ‏16 يبين ايجاد أول كلمة صحيحه

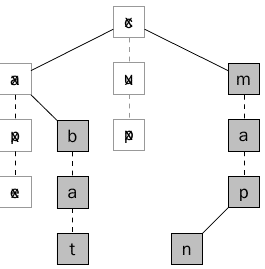
وسوف تستمر هذه العملية الى ايجاد كل النصوص المطابقة (سوف يتم تجربة العقدة c و m)، الشكل التالي يبين الكلمات المطابقة وغير المطابقة .

الشكل ‏17 يبين كل الكلمات المطابقة وغير المطابقة

والكلمات التي تم ايجادها هي bat و man و map ، وتم ذلك في خلال 11 مقارنه فقط، وفي حال كنا استخدمنا طريقة الBrute Force لأيجاد كل الكلمات المطابقة للنمط –a- سيكون هناك (26*26 احتمال) وبالتالي الكثير من المقارنات (676 مقارنة).

تطبيق الTernary Search Tree Implementation:

// Ternary search tree

#include <iostream>
#include <vector>
using namespace std;

#define WILDCARD '?'

class Node {
	private:
		char c;
		Node *smaller,*larger,*child;
		string word;

	public:
		Node(char ch) { c = ch; smaller=larger=child=NULL; word="";}

		char getChar()	 { return c; }
		Node* getSmaller() { return smaller; }
		Node* getLarger()  { return larger; }
		Node* getChild()   { return child; }
		string getWord()   { return word; }

		void setSmaller (Node* n) { smaller = n; }
		void setLarger  (Node* n) { larger  = n; }
		void setChild   (Node* n) { child   = n; }
		void setWord	(const string& s) { word = s; }

		bool isEndOfWord() { 
			return getWord() != "";
		}
};

class TernarySearchTree {
	private:
		Node* root;

	public:
		TernarySearchTree () : root(NULL) { }

		void add(const string& str) {
			Node* node = insert(root,str,0);
			if ( root == NULL )
				root = node;
		}

		bool contain (const string& word) {
			Node* node = search(root,word,0);
			return node != NULL && node->isEndOfWord();
		}

		void prefixSearch(const string& prefix, vector<string>& result) {
			inOrderTraversal(search(root,prefix,0),result);
		}

		void patternMatch(const string& pattern , vector<string>& result) {
			patternMatch(root,pattern,0,result);
		}

	private:
		Node* search( Node* node, const string& word, unsigned int index) {
			if ( node == NULL)
				return NULL;

			char ch = word[index];

			if ( ch == node->getChar()){
				if ( index+1 < word.length() ) {
					node =search(node->getChild(),word,index+1);
				}
			}
			else if ( ch < node->getChar() )
				node = search(node->getSmaller(),word,index);
			else
				node = search(node->getLarger(),word,index);

			return node;
		}

		Node* insert(Node* node,const string& word,unsigned int index) {
			char c = word[index];

			if ( node == NULL )
				node = new Node(c);

			if ( c == node->getChar() ) {
				if ( index+1 < word.length() )
					node->setChild(insert(node->getChild(),word,index+1));
				else
					node->setWord(word);
			}
			else if ( c < node->getChar() ) 
				node->setSmaller(insert(node->getSmaller(),word,index));
			else
				node->setLarger(insert(node->getLarger(),word,index));

			return node;
		}

		void patternMatch (Node* node,const string& pattern,unsigned int index,vector<string>& result){
			if ( node == NULL)
				return;

			char c = pattern[index];

			if ( (c == WILDCARD) || (c < node->getChar()) )
				patternMatch(node->getSmaller(),pattern,index,result);

			if ( (c == WILDCARD) || (c == node->getChar() ) ){
				if ( index+1 < pattern.length())
					patternMatch(node->getChild(),pattern,index+1,result);
				else if ( node->isEndOfWord() )
					result.push_back(node->getWord());
			}

			if ( (c== WILDCARD) || (c > node->getChar()) )
				patternMatch(node->getLarger(),pattern,index,result);
		}

		void inOrderTraversal(Node* node,vector<string>& result) {
			if ( node == NULL )
				return;

			inOrderTraversal(node->getSmaller(),result);

			if (node->isEndOfWord() )
				result.push_back(node->getWord() );

			inOrderTraversal(node->getChild(),result);
			inOrderTraversal(node->getLarger(),result);
		}
};

int main (int argc , char* argv[]) {
	TernarySearchTree tst;

	// test add 
	tst.add("prefabricate");
	tst.add("presume");
	tst.add("prejudice");
	tst.add("preliminary");
	tst.add("apple");
	tst.add("ape");
	tst.add("appeal");
	tst.add("car");
	tst.add("dog");
	tst.add("cat");
	tst.add("mouse");
	tst.add("mince");
	tst.add("minty");

	//test contain
	cout << ( tst.contain("prefabricate") ? "found " : "not found " )
		 << "prefabricate" << endl;

	cout << ( tst.contain("presume") ? "found " : "not found " )
		 << "presume" << endl;

	cout << ( tst.contain("prejudice") ? "found " : "not found " ) 
		 << "prejudice" << endl;

	cout << ( tst.contain("cat") ? "found " : "not found " ) 
		 << "cat" << endl;

	cout << ( tst.contain("minty") ? "found " : "not found " ) 
		 << "minty" << endl;

	cout << ( tst.contain("pre") ? "found " : "not found " ) 
		 << "pre" << endl;

	cout << ( tst.contain("dogs") ? "found " : "not found " ) 
		 << "dogs" << endl;

	cout << ( tst.contain("UNKNOWN") ? "found " : "not found " ) 
		 << "UNKNOWN" << endl;

	// test prefix
	string prefix = "pre";
	cout << endl;
	cout << "Found All Word Begin with: " << prefix << endl;
	vector<string> words;
	tst.prefixSearch(prefix,words);
	for (unsigned int i=0; i<words.size(); i++)
		cout << words[i] << endl;

	// test pattern matching
	string pattern = "m???e";
	cout << endl;
	cout << "Found All Word same : " << pattern << endl;
	vector<string> lists;
	tst.patternMatch(pattern,lists);
	for (unsigned int i=0; i<lists.size(); i++)
		cout << lists[i] << endl;

	return (0);
}

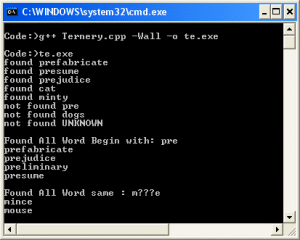
وعند تنفيذ البرنامج سوف يتم طباعه الكلمات التي نبحث عنها باستخدام الدالة contain ، ثم تتم طباعه جميع الكلمات التي تبدأ بالأحرف pre ، ثم تتم طباعه كل الكلمات التي لها النمط m???e كما يوضح ذلك شكل المخرج (18) .

الشكل ‏18 يبين مخرج تنفيذ البرنامج السابق.

خاتمة

لا تكاد تخلو البرامج التي نستخدمها من أحد الهياكل القويه، والشجره التي تناولناها في هذه المقالة تستخدم كثيرا في البرامج والIDE والتي تعرض كل الدوال والتي تبدأ بالحرف الذي تقوم بكتابته ، محرك Google يستخدم هذه الخوارزمية لكي يخرج جميع الكلمات التي تبدأ بالحرف الذي تكتبه في الصندوق ..تطبيق أخر لها مثلا في حل لعبه الكلمات المتقاطعه Crossword حيث ستبحث في قاعده بيانات الكلمات عن كلمة مكون من عدد من الأحرف ؟؟؟ ويكون الحرف الثاني منها هو الحرف الثالث في الكلمة ؟؟ وهكذا من شروط .. وستحل اللعبه في غضون ثواني .